- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:48.
- Laatst gewijzigd 2025-01-23 12:42.
Snelheid is een berekening van hoe snel iets in één keer beweegt. Als je ooit naar de snelheidsmeter van een rijdende auto hebt gekeken, zie je de snelheid tellen - hoe verder de naald beweegt, hoe hoger de snelheid van het voertuig. Er zijn verschillende manieren om de snelheid te berekenen, afhankelijk van het soort informatie dat je hebt. In het algemeen is de formule snelheid = afstand/tijd (of k = j/w) is de gemakkelijkste manier om de snelheid te berekenen.
Stap
Methode 1 van 3: Standaardsnelheidsberekeningsformules gebruiken

Stap 1. Zoek de afstand die een object heeft afgelegd
De basisformule die de meeste mensen gebruiken om de snelheid van iets te vinden, is heel gemakkelijk te gebruiken. Allereerst moet u weten "hoeveel afstand heeft het gemeten object afgelegd". Met andere woorden, wat is de afstand tussen het beginpunt en het eindpunt van het object?
Deze formule is gemakkelijker te begrijpen aan de hand van een voorbeeld. Laten we zeggen dat we met de auto naar een speeltuin reizen voor "161 kilometer". In een paar stappen kunnen we deze informatie gebruiken om de berekening van de formule te voltooien

Stap 2. Zoek de tijd die het object nodig heeft om die afstand af te leggen
De volgende informatie die u nodig hebt, is hoe lang het duurt voordat het object een bepaalde afstand heeft bereikt. Met andere woorden, hoe lang duurt het voordat het object van het beginpunt naar het eindpunt beweegt?
Laten we in dit voorbeeld zeggen dat het object ca. twee uur om op de bestemming te komen.

Stap 3. Deel de afstand door de tijd die nodig is om de snelheid van het object te vinden
Je hebt alleen deze twee stukjes informatie nodig om de snelheid van het object te kennen. De afstand tot de tijd is gelijk aan de snelheid van het object.
In dit voorbeeld 161 kilometer/2 uur = 80,5 kilometer/uur.

Stap 4. Vergeet de gebruikte eenheid niet
Het is erg belangrijk om de juiste eenheden in je antwoord te gebruiken (zoals kilometers per uur, etc.) Zonder deze eenheden is het erg moeilijk voor mensen om de betekenis van uw antwoord te begrijpen. Je kunt ook punten verliezen als je de verkeerde eenheid gebruikt bij het maken van opdrachten van school.
De eenheid van snelheid is eenheid van afstand tot tijdseenheid. Omdat we bijvoorbeeld afstand in kilometers en tijd in uren meten, zijn de gebruikte eenheden: kilometer/uur (of kilometers per uur).
Methode 2 van 3: Moeilijkere berekeningen oplossen

Stap 1. Zoek verschillende variabelen om het probleem van afstand en tijd op te lossen
Zodra u de basisformule voor snelheid begrijpt, kunt u deze gebruiken om andere berekeningen dan snelheid uit te voeren. Als u bijvoorbeeld in eerste instantie alleen de snelheid van het object en één andere variabele kent, kunt u de bovenstaande formule herschikken om de onbekende informatie te vinden.
-
Laten we bijvoorbeeld zeggen dat we weten dat een trein vier uur lang 20 kilometer per uur rijdt, maar we weten niet hoe ver hij heeft afgelegd. Om erachter te komen, kunnen we de formule op de volgende manier herschikken:
-
- snelheid = afstand/tijd
- snelheid × tijd = (afstand/tijd) × tijd
- snelheid × tijd = afstand
- 20 km/uur × 4 uur = afstand = 80 kilometer
-

Stap 2. Converteer de eenheden die u gebruikt naar behoefte
Soms kunt u de snelheid berekenen met een bepaalde eenheid, maar deze moet u omrekenen naar een andere eenheid. In dit geval moet u een conversiefactor gebruiken om het antwoord volgens de juiste eenheden te krijgen. Om dit te doen, schrijft u eenvoudig de relatie tussen de eenheden in breukvorm en vermenigvuldigt u deze. Draai bij vermenigvuldigen de breuk zo nodig om om ongewenste eenheden te verwijderen. Deze methode is veel eenvoudiger dan het klinkt!
-
Laten we bijvoorbeeld zeggen dat we in het bovenstaande voorbeeldprobleem het antwoord in mijlen in plaats van kilometers nodig hebben. Een mijl is gelijk aan ongeveer 1,6 kilometer. We kunnen de conversie dus als volgt doen:
-
- 80 kilometer × 1 mijl/1,6 kilometer = 50 mijl
-
- Onthoud dat, omdat kilometers onderaan de breuk verschijnen, kilometers worden verwijderd uit het vorige antwoord, dus het uiteindelijke resultaat gebruikt mijlen.
- Deze website biedt conversiefuncties voor de meeste veelgebruikte eenheden.

Stap 3. Vervang indien nodig de variabele "afstand" door de afstandsformule
Objecten bewegen niet altijd in een recht, vloeiend pad. Als dit waar is, kunt u mogelijk niet eenvoudig een numerieke waarde invoeren als een eenheid van afstand in de standaardsnelheidsformule. Het is echter mogelijk dat u de letter j in de formule k = j/w moet vervangen door een formule die lijkt op de afstand die het object heeft afgelegd.
-
Laten we bijvoorbeeld zeggen dat een vliegtuig 5 keer door de lucht draait over een afstand van 20 mijl. Het vliegtuig voltooide de ronde in een half uur. In dit voorbeeld moeten we nog steeds de totale afstand vinden die het vliegtuig heeft afgelegd voordat we de snelheid kunnen bepalen. We kunnen de formule gebruiken voor het berekenen van de afstand rond een cirkel (afstand eromheen) in plaats van j in deze formule. Deze formule is omtrek = 2πr waarbij r = cirkelstraal. Hier is hoe het op te lossen:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 mijl/uur
-

Stap 4. Begrijp dat k = j/w de gemiddelde snelheid geeft
De gemakkelijke en eenvoudige formule die we gebruiken om de snelheid te vinden, heeft één nadeel. De resulterende waarde is technisch gezien de gemiddelde snelheid. Dit betekent dat de formule ervan uitgaat dat het object dat je meet dezelfde snelheid gebruikt als het beweegt. Zoals we hieronder zullen zien, zal het veel moeilijker zijn om de snelheid van een object in een enkel moment te vinden.
Om dit verschil te illustreren, stelt u zich de laatste keer dat u met de auto reisde voor. Het is onwaarschijnlijk dat u met dezelfde snelheid reist als u reist. U begint uw reis echter meestal met een lage snelheid en voert onderweg geleidelijk uw snelheid op, waarbij u stopt vanwege rode lichten, files, enz. Als u de standaardsnelheidsformule gebruikt om de snelheid tijdens het rijden te bepalen, kunnen wijzigingen in die snelheid niet worden gedetecteerd. U krijgt echter een antwoord dat de gemiddelde snelheid laat zien van alle snelheidsverschillen die u aflegt
Methode 3 van 3: Onmiddellijke snelheid berekenen
Opmerking:
In dit gedeelte worden technieken gebruikt die minder bekend zijn bij mensen die nog nooit wiskunde hebben gestudeerd. Lees onze artikelen over calculus voor hulp.
Stap 1. Begrijp dat snelheid wordt gedefinieerd als de snelheid van versnelling
Snelheidsberekeningen op hoog niveau zijn nogal verwarrend omdat wiskundigen en wetenschappers verschillende definities gebruiken om "snelheid" en "versnelling" te beschrijven. Versnelling heeft twee componenten: een "snelheid" en een "richting". De snelheid is gelijk aan de snelheid van het object. Een verandering van richting zal een verandering in versnelling veroorzaken, maar geen verandering in snelheid.
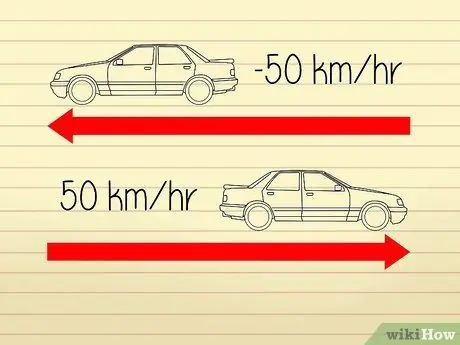
- Laten we bijvoorbeeld zeggen dat twee auto's in tegengestelde richting rijden. De snelheidsmeters op beide auto's geven een cijfer van 50 km/u aan, dus ze rijden allebei met dezelfde snelheid. Omdat de auto's echter uit elkaar rijden, kunnen we zeggen dat een van de auto's een "versnelling" van -50 km/u heeft, terwijl de andere een "versnelling" van 50 km/u heeft.
- Net als ogenblikkelijke snelheidsberekeningen, kunt u ook ogenblikkelijke versnellingsberekeningen uitvoeren.

Stap 2. Gebruik absolute waarden om negatieve versnelling te meten
Een object kan een negatieve versnelling hebben (als het in een negatieve richting beweegt ten opzichte van een ander object). Er is echter geen negatieve snelheid. Dus in dit geval geeft de absolute waarde van de snelheid de snelheid van het object aan.
Om deze reden hebben beide auto's in het bovenstaande voorbeeldprobleem een snelheid van 50 km/u.
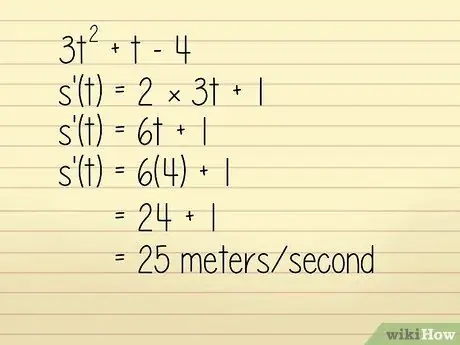
Stap 3. Neem de afgeleide van de positie van de functie
Als je een functie k(w) hebt die de positie van een object laat zien zonder dat je de tijd hoeft te berekenen, dan zal de afgeleide van k(w) de versnelling laten zien zonder dat timing nodig is. Steek gewoon de tijdwaarde in deze formule zodat de variabele w (of welke tijdswaarde dan ook wordt gebruikt) wordt versneld volgens die tijd. Vanaf hier kun je gemakkelijk de snelheid van het object vinden.
-
Laten we bijvoorbeeld zeggen dat de positie van een object op één meter wordt beschreven in de vergelijking 3q2 + w - 4 waarbij w = tijd in seconden. We willen de snelheid van het object weten bij w = 4 seconden. In dit geval kunt u het oplossen door:
-
- 3w2 +w - 4
- k'(w) = 2 × 3w + 1
- k'(w) = 6w + 1
-
-
Nu voeren we w = 4 in:
-
- k'(w) = 6(4) + 1 = 24 + 1 = 25 meter/seconde. Technisch gezien is dit een berekening van de versnelling, maar aangezien deze positief is en de richting niet in de vraag wordt genoemd, kunnen we deze gebruiken om de snelheid te vinden.
-

Stap 4. Neem de integrale versnellingsfunctie
Versnelling is een manier om de verandering in de versnelling van een object in de tijd te meten. Dit onderwerp is te complex om in dit artikel volledig te worden uitgelegd. Het is echter handig om op te merken dat wanneer u een functie a(w) hebt die versnelling vertegenwoordigt met betrekking tot tijd, de integraal van a(w) het resultaat van versnelling zal retourneren op basis van die tijd. Onthoud dat het erg handig is om de initiële versnelling van een object te kennen, zodat je de constante van dat resultaat kunt definiëren uit een oneindige integraal.
-
Laten we bijvoorbeeld zeggen dat een object een constante versnelling heeft (in m/s2 als resultaat van a(w) = -30. Zeg ook dat het object een initiële versnelling heeft van 10 m/s. We moeten de snelheid vinden bij w = 12 seconden. In dit geval kunnen we het oplossen door:
-
- a(w) = -30
- p(w)= a(w)dw = -30dw = -30w + C
-
-
Om C te vinden, lossen we p(w) op voor w = 0. Onthoud dat de initiële versnelling van het object 10 m/s is.
-
- p(0) = 10 = -30(0) + C
- 10 = C, dus p(w) = -30w + 10
-
-
Nu kunnen we w = 12 seconden invoeren.
-
- p(12) = -30(12) + 10 = -360 + 10 = -350. Omdat snelheid een absolute waarde van versnelling is, is de snelheid van het object 350 meter/seconde.
-
Tips
- Oefening maakt goed! Probeer uw eigen vraag te maken door de getallen in het bovenstaande voorbeeldprobleem te vervangen.
- Als u op zoek bent naar een snelle manier om calculus te oefenen voor een betere rekensnelheid, gebruik dan de online afgeleide rekenmachine hier en de online integraalcalculator hier.






