- Auteur Jason Gerald [email protected].
- Public 2024-02-01 14:14.
- Laatst gewijzigd 2025-01-23 12:42.
Het enige dat u nodig hebt om de gemiddelde snelheid te berekenen, is de totale verplaatsing. of verandering van positie, en totale tijd. Onthoud dat snelheid ook de richting en snelheid van een object berekent, dus neem een richting op in je antwoord, zoals 'noord', 'voorkant' of 'links'. Als uw snelheidsberekeningsprobleem ook constante acceleratie betreft, kunt u een snelle manier leren om het antwoord nog gemakkelijker te vinden.
Stap
Methode 1 van 2: Berekening van de gemiddelde verplaatsingssnelheid en tijd

Stap 1. Onthoud dat snelheid zowel de snelheid als de richting van een object omvat
Velocity beschrijft de snelheid waarmee de positie van een object verandert. Dit heeft niet alleen te maken met hoe snel het object beweegt, maar ook met zijn richting. '100 meter per seconde zuidwaarts' is een andere snelheidswaarde dan '100 meter per seconde oostwaarts'.
- Grootheden die richting hebben, worden vectorgrootheden genoemd. Deze grootheid kan worden onderscheiden van een richtingloze grootheid die een scalaire grootheid wordt genoemd door een pijl boven de variabele te schrijven. De notatie v vertegenwoordigt bijvoorbeeld de snelheid, terwijl de notatie v → staat voor snelheid of snelheid + richting. De v-notatie die in dit artikel wordt gebruikt, staat voor snelheid.
- Bij wetenschappelijke problemen moet je meters of andere metrische eenheden gebruiken om afstand uit te drukken, terwijl je voor alledaagse doeleinden elke gewenste eenheid kunt gebruiken.
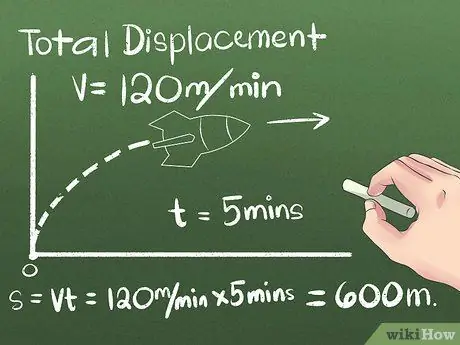
Stap 2. Zoek de totale verplaatsingswaarde
Verplaatsing is de verandering in de positie van een object, of de afstand en richting tussen het begin- en eindpunt. De richting waarin het object beweegt voordat het zijn uiteindelijke positie bereikt, kan worden verwaarloosd, omdat alleen rekening wordt gehouden met de afstand tussen het begin- en eindpunt. Voor het eerste voorbeeld gebruiken we een object dat met een constante snelheid in één richting beweegt:
- Stel dat een raket 5 minuten naar het noorden beweegt met een constante snelheid van 120 meter per minuut. Om de uiteindelijke positie te berekenen, gebruikt u de formule s = vt, of gebruikt u praktisch denken om de afstand te berekenen die de raket daarna heeft afgelegd (5 minuten) (120 meter/minuut) = 600 meter noord vanaf het startpunt.
- Voor problemen met constante versnelling, kun je ze oplossen met s = vt + at2, of gebruik de korte methode die in een andere sectie wordt beschreven om het antwoord te vinden.
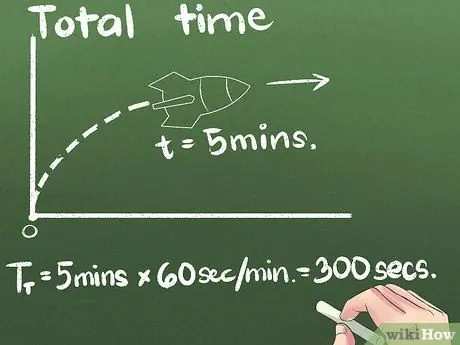
Stap 3. Zoek de totale bestede tijd
In ons voorbeeld beweegt de raket 5 minuten vooruit. Je kunt de gemiddelde snelheid in elke tijdseenheid uitdrukken, maar de tweede is de internationale wetenschappelijke standaardeenheid. In dit voorbeeld veranderen we de eenheden van seconden: (5 minuten) x (60 seconden/minuut) = 300 seconden.
Zelfs bij wetenschappelijke problemen, als de vraag het uur of een grotere tijdseenheid gebruikt, is het gemakkelijker om eerst de snelheid te berekenen en vervolgens het uiteindelijke antwoord om te zetten in meters/seconde
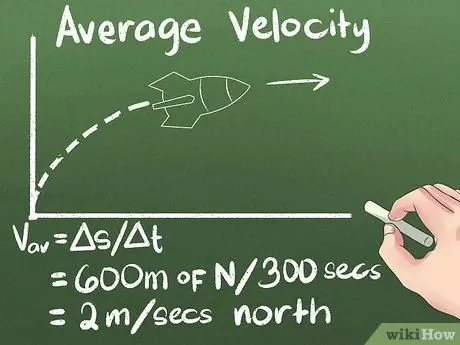
Stap 4. Bereken de gemiddelde snelheid als verplaatsing in de tijd
Als je weet hoe ver een object beweegt en hoe lang het duurt om daar te komen, weet je hoe snel het beweegt. Dus voor het voorbeeld dat we gebruiken, is de gemiddelde snelheid van de raket (600 meter noord) / (300 seconden) = 2 meter/seconde noord.
- Vergeet niet een richting op te nemen (zoals 'voorkant' of 'noord').
- In de formule vav = s/Δt. Het delta-symbool betekent 'verandering', dus s/Δt betekent 'verandering van positie over een bepaalde periode'.
- De gemiddelde snelheid kan worden geschreven als vav, of als een v met een horizontale lijn erboven.

Stap 5. Los meer gecompliceerde problemen op
Als een object van richting of snelheid verandert, raak dan niet in de war. De gemiddelde snelheid wordt nog steeds "slechts" berekend uit de totale verplaatsing en de totale tijd. Wat er gebeurt tussen het begin- en eindpunt kun je negeren. Hieronder volgen enkele voorbeelden van een object dat reist met dezelfde verplaatsing en totale tijd, en dus dezelfde gemiddelde snelheid:
- Anna loopt 2 seconden met 1 meter/s naar het westen, versnelt dan plotseling naar 3 meter/seconde en blijft 2 seconden naar het westen lopen. De totale verplaatsing is (1 m/s westwaarts) (2 sec) + (3 m/s westwaarts) (2 sec) = 8 meter westwaarts. De totale tijd is 2 seconden + 2 seconden = 4 seconden. Dus de gemiddelde snelheid is 8 meter west/ 4 seconden = 2 meter/seconde west.
-
Bart loopt 3 seconden met 5 meter/sec naar het westen, draait zich dan om en loopt 1 seconde met 7 meter/sec naar het oosten. We kunnen de oostwaartse beweging zien als "negatieve westwaartse beweging", dus de totale verplaatsing is = (5 meter/sec westwaarts) (3 sec) + (-7 m/s westwaarts) (1 sec) = 8 meter. Totale tijd = 4 seconden. Gemiddelde snelheid = 8 meter west / 4 seconden = 2 meter/seconde west.
-
Charlotte liep 1 meter naar het noorden en vervolgens 8 meter naar het westen en vervolgens 1 meter naar het zuiden. De tijd die nodig is om de hele reis te voltooien is 4 seconden. Teken het diagram op een stuk papier en je zult zien dat het eindpunt 8 meter ten westen van het startpunt ligt, dus deze waarde is de verplaatsing. De totale tijd die het kost is 4 seconden, dus de gemiddelde snelheid is 8 meter west / 4 seconden = 2 meter/seconde west.
Methode 2 van 2: Berekening van de gemiddelde snelheid van vaste versnelling

Bereken de gemiddelde snelheid Stap 6 Stap 1. Overweeg de beginsnelheid en constante versnelling
Laten we zeggen dat ons probleem is: "Een fiets beweegt naar rechts met een snelheid van 5 m/s, met een constante versnelling van 2 m/s2. Als deze fiets 5 seconden beweegt, wat is dan zijn gemiddelde snelheid?"
Als de eenheid "meter/seconde"2" om je te verwarren, schrijf het als "meter/seconde/seconde" of "meters per seconde per seconde." Een versnelling van 2 meter/seconde/seconde betekent dat de snelheid elke seconde met 2 meter per seconde toeneemt.

Bereken gemiddelde snelheid Stap 7 Stap 2. Gebruik versnelling om de eindsnelheid te vinden
Versnelling, aangeduid met de notatie a, is de snelheid waarmee de snelheid (of snelheid) verandert. De snelheid neemt toe met een constante snelheid. U kunt een tabel tekenen met versnelling om de snelheid op verschillende tijdstippen tijdens de fietsreis te vinden. We moeten deze tabel maken om het eindpunt van het probleem te vinden (op t = 5 seconden), maar we zullen een langere tabel maken om het u gemakkelijker te maken dit concept te begrijpen:
- Op het startpunt (tijd t = 0 seconden) rijdt de fiets met een snelheid van 5 meter/s.
- Na 1 seconde (t = 1) rijdt de fiets met een snelheid van 5 meter/seconde + bij = 5 meter/seconde + (2 meter/seconde2)(1 seconde) = 7 meter/seconde.
- Op t = 2 beweegt de fiets naar rechts met een snelheid van 5+(2)(2) = 9 meter/sec.
- Op t = 3 gaat de fiets naar rechts met een snelheid van 5+(2)(3) = 11 meter/sec.
- Op t = 4 gaat de fiets naar rechts met een snelheid van 5+(2)(4) = 13 meter/sec.
- Op t = 5 gaat de fiets naar rechts met een snelheid van 5+(2)(5) = 15 meter/seconde.

Bereken gemiddelde snelheid Stap 8 Stap 3. Gebruik deze formule om de gemiddelde snelheid te vinden
Als en "alleen" als de versnelling constant is, zal de gemiddelde snelheid gelijk zijn aan de gemiddelde waarde van de som van de eind- en beginsnelheden. (vF +vl)/2. Voor ons voorbeeldprobleem hierboven is de beginsnelheid van de fiets vl 5 meter/seconde. Nadat we hebben berekend, is de eindsnelheid vF 15 meter/seconde. Als we deze twee waarden bij elkaar optellen, krijgen we (15 meter/seconde + 5 meter/seconde) / 2 = (20 meter/seconde) / 2 = 10 meter/seconde juiste richting.
- Vergeet niet om de richting op te nemen, in dit geval 'goed'.
- Deze term kan worden geschreven als v0 (snelheid op tijdstip 0, of beginsnelheid) en v (eindsnelheid).

Bereken gemiddelde snelheid Stap 9 Stap 4. Begrijp de formule van de gemiddelde snelheid intuïtief
Om de gemiddelde snelheid te vinden, kunnen we de snelheid op elk punt gebruiken en het gemiddelde voor al deze punten vinden. (Dit is de definitie van een gemiddelde.) Aangezien dit calculus of oneindige tijd vereist, moet u deze formule intuïtiever begrijpen. In plaats van elke tijd te nemen, bereken je de gemiddelde snelheid van de twee tijdstippen en bekijk je de resultaten. Een punt in de tijd is dichtbij het begin van de rit, waar de fiets langzaam gaat, en een ander punt is dichtbij het eindpunt waar de fiets snel gaat.

Bereken gemiddelde snelheid Stap 10 Stap 5. Test de intuïtieve theorie
Gebruik de bovenstaande tabel om de snelheid op verschillende tijdstippen te bepalen. Sommige paren die aan onze criteria voldoen, zijn (t=0, t=5), (t=1, t=4) of (t=2, t=3). Je kunt deze formule ook testen met andere t-waarden dan gehele getallen, als je wilt.
Welk paar punten je ook kiest, de gemiddelde snelheid op dat moment zal altijd hetzelfde zijn. Bijvoorbeeld ((5+15)/2), ((7+13)/2), of ((9+11)/2) zijn allemaal gelijk aan 10 meter/sec naar rechts

Bereken gemiddelde snelheid Stap 11 Stap 6. Vul de intuïtieve uitleg in
Als we deze methode gebruiken met een lijst van elke afgelegde tijd, gaan we verder met het berekenen van het gemiddelde van de eerste helft van de reis en de tweede helft van de reis. De tijd die nodig is om elke helft af te leggen is hetzelfde, dus er gaat geen snelheid verloren als we klaar zijn met tellen.
- Aangezien elk paar hetzelfde resultaat zal geven, zal het gemiddelde van deze snelheden ook dezelfde waarde hebben. In ons voorbeeld is de snelheid van het geheel "10 meter/sec naar rechts" nog steeds 10 meter/sec naar rechts.
- We kunnen deze waarde vinden door het gemiddelde van elk paar te berekenen, bijvoorbeeld de begin- en eindsnelheden. In ons voorbeeld worden deze snelheden bereikt op t=0 en t=5, en kunnen ze berekend worden met de formule hierboven: (5+15)/2 = 10 meter/sec naar rechts.

Bereken gemiddelde snelheid Stap 12 Stap 7. Begrijp deze formule wiskundig
Als u meer vertrouwd bent met bewijzen die als formules zijn opgeschreven, kunt u beginnen met een formule om de afgelegde afstand te berekenen uitgaande van constante versnelling, en de formule daaruit afleiden:
- s = vlt + at2. (Technisch gezien s en t, of verandering van positie en verandering in de tijd, maar je zou ook begrepen worden als je s en t zou schrijven.)
- gemiddelde snelheid vav gedefinieerd als s/t, dus voer de formule in de vorm s/t in.
- vav = s/t = vl + bij
- Versnelling x tijd is gelijk aan de verandering in totale snelheid, of vF - vl. Dus we kunnen "at" in de formule vervangen en krijgen:
- vav = vl + (vF - vl).
- vereenvoudigen: vav = vl + vF - vl = vl + vF = (vF +vl)/2.
Tips
- Snelheid is anders dan snelheid omdat snelheid een vectorgrootheid is, terwijl snelheid een scalaire grootheid is. Vectorgrootheden hebben betrekking op zowel richting als grootte, terwijl scalaire grootheden alleen betrekking hebben op grootte.
- Als het object in één dimensie beweegt, zoals links-rechts, kunt u een positief getal gebruiken om één richting aan te geven (zoals rechts) en een negatief getal om een andere richting aan te geven (links). Schrijf deze notatie bovenaan je pagina, zodat het duidelijk is voor mensen die je werk lezen.






