- Auteur Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Laatst gewijzigd 2025-01-23 12:42.
Plaatswaarde, of het concept dat de waarde van een getal (0-9) wordt bepaald door zijn positie in een bepaald getal, is een fundamenteel concept in de wiskunde. Omdat dit concept zo gemakkelijk is voor mensen die het al begrijpen, kan het behoorlijk ingewikkeld zijn om het te onderwijzen. Zodra studenten dit concept echter begrijpen, zullen ze klaar en enthousiast zijn om hun nieuwe vaardigheden te gebruiken en complexere wiskundige concepten te leren.
Stap
Deel 1 van 3: Introductie van de basisconcepten

Stap 1. Neem de tijd om plaatswaarde aan te leren
Als je lesgeeft binnen een vooraf gedefinieerd leerplan, zou je al een idee moeten hebben van hoe je plaatswaarde in een breder scala van leren kunt passen. Als je thuis bijles geeft of lesgeeft, is de leerstructuur flexibeler. Plan om plaatswaarde te onderwijzen ergens nadat studenten klaar zijn met tellen en het uitvoeren van eenvoudige optel- en aftrekbewerkingen - meestal rond graad 1 of graad 2. Een begrip van plaatswaarde zal deze kinderen een basis bieden om complexere wiskundige concepten te begrijpen.

Stap 2. Introduceer het concept van het tellen van groepen getallen
De meeste kinderen van de kinderen leren alleen de getallen één voor één tellen: één… twee… drie… vier. Dit is voldoende voor elementair optellen en aftrekken, maar nog te eenvoudig om een solide basis te bieden voor het begrijpen van complexere functies. Voordat je ze leert hoe ze grote getallen kunnen opsplitsen in hun respectievelijke plaatswaarden, is het een goed idee om ze te leren een groep kleine getallen op te splitsen in grote getallen.
- Leer uw leerlingen hoe ze twee twee, drie drie, vijf vijf en tien tien tellen. Dit is een fundamenteel concept dat leerlingen moeten begrijpen voordat ze leren over plaatswaarde.
- Probeer vooral een sterke "sensatie van tientallen" op te bouwen. Moderne wiskunde gebruikt het getal tien als basis, waardoor het voor kinderen gemakkelijker wordt om complexere systemen te leren als ze eraan wennen om op deze manier te denken. Leer uw leerlingen om instinctief getallen te groeperen in sets van tien.

Stap 3. Herzie het concept van plaatswaarde
Verfris uw begrip. Zorg ervoor dat u dit concept zelf volledig begrijpt voordat u het aan een groep jonge studenten probeert te onderwijzen. Simpel gezegd, plaatswaarde is het idee dat de waarde van een getal (0-9) afhangt van zijn "plaats" of positie in een getal.

Stap 4. Leg het verschil uit tussen getallen en getallen
Getallen zijn symbolen van de tien basisgetallen waaruit alle getallen bestaan: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Deze getallen worden gecombineerd om alle andere getallen te vormen. Een nummer kan een nummer zijn (bijvoorbeeld het nummer 7), maar alleen als het niet gegroepeerd is met andere nummers. Wanneer twee of meer getallen bij elkaar worden gegroepeerd, vormt de volgorde van de getallen het grotere getal.
Laat zien dat op zichzelf "1" het nummer één is en "7" het nummer zeven. Wanneer gegroepeerd als "17", vormen de twee getallen het getal zeventien. Evenzo vormen "3" en "5" samen het getal vijfendertig. Laat enkele andere voorbeelden zien zodat de leerlingen begrijpend naar huis kunnen gaan
Deel 2 van 3: Lesgeven door visuele voorbeelden
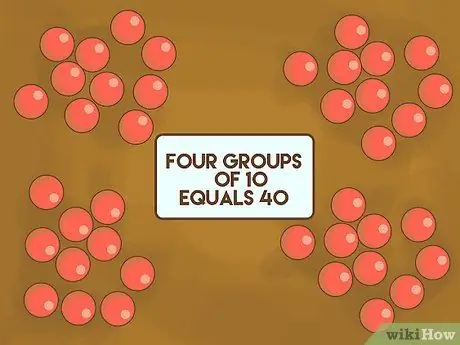
Stap 1. Laat de kinderen zien dat tien tot tien tellen makkelijker is
Gebruik 30 - 40 objecten die klein, telbaar en redelijk homogeen zijn. Bijvoorbeeld: kiezels, knikkers of een gum. Spreid het uit op de tafel voor de leerlingen. Leg uit dat we in de moderne wiskunde het getal 10 als basis gebruiken. Schik de voorwerpen in verschillende groepen en tel ze dan voor de klas. Laat ze zien dat vier groepen van 10 kiezelstenen gelijk zijn aan 40.

Stap 2. Vertaal het voorbeeld met kiezels in geschreven cijfers
Schrijf de conceptschets op het bord. Maak eerst een gewone T-kaart. Schrijf het cijfer 1 in de rechterbovenhoek van het T-diagram. Schrijf vervolgens het cijfer 10 in de linkerbovenhoek. Schrijf een 0 in de rechterkolom met het label "1" en schrijf een 4 in de linkerkolom met het label "10". Nu kun je de klas uitleggen dat elk nummer gemaakt met kiezelstenen zijn eigen "plaats" heeft.
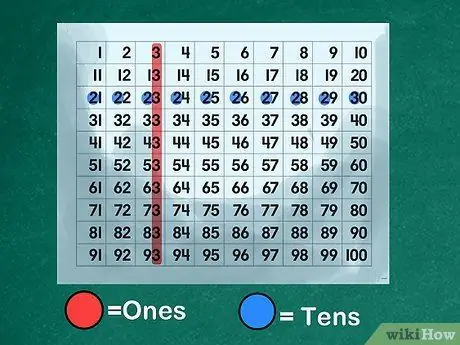
Stap 3. Gebruik een numeriek toetsenblok om de basis van de plaatswaarde te illustreren
Maak of print een "numeriek toetsenblok" dat alle getallen in de volgorde van 1 tot 100 weergeeft. Laat de leerlingen zien hoe de getallen 0 tot 9 interageren met de getallen 10 tot 100. Leg uit dat elk getal van 10 tot 99 uit twee cijfers bestaat, een een nummer in de "enen" plaats en een ander nummer in de "tientallen". Laat zien dat het getal "4" staat voor "vier" wanneer het op de plaats "enen" staat, maar dient als voorvoegsel voor het getal "40" wanneer het op de plaats "tientallen" staat.
- Illustreer de plaats van "eenheden". Geef de klas opdracht om alle getallen te noemen met het cijfer "3" in de plaats "enen": 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Leg uit wat de plaats van de "tientallen" is. Instrueer de leerlingen om alle getallen aan te duiden die een "2" hebben in plaats van "tientallen": 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Leg uit dat de "3" in "23" is gestapeld bovenop " 20" gemarkeerd met het nummer "2." Leer uw kinderen om de plaats "tientallen" te lezen als een trigger om te leren.

Stap 4. Experimenteer met andere visuele leermiddelen
Je kunt fysieke objecten rangschikken of ze op het bord tekenen. Je kunt de plaatswaarde uitleggen door incrementen van geldwaarde te gebruiken, die studenten mogelijk al hebben bestudeerd, om ze te relateren aan geschaalde numerieke waarden. Probeer voor een leuke en interactieve activiteit de leerlingen zelf als 'groepswaarde' te gebruiken.
Het menselijk geheugen wordt gedomineerd door visuele dingen, dus het concept van plaatswaarde is nog steeds abstract totdat je het visueel kunt maken. Ondertussen kunnen numerieke symbolen zelf nog steeds abstract zijn voor kinderen! Zoek naar manieren om groepen te tellen en waardeactiviteiten zo te plaatsen dat ze eenvoudig, tastbaar en intuïtief zijn
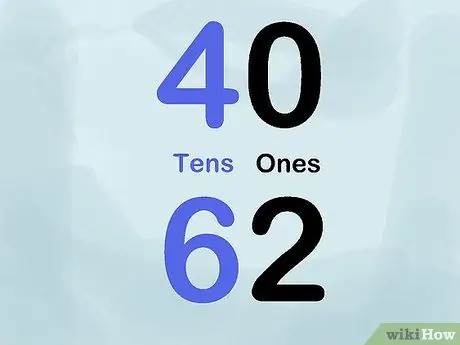
Stap 5. Gebruik kleur
Probeer verschillende kleuren krijt of stiften te gebruiken om de plaatswaarde aan te tonen. Schrijf bijvoorbeeld verschillende getallen met een zwarte stift voor de "enen"-plaats en een blauwe markering voor de "tientallen". U zou dus 40 schrijven met het cijfer "4" in blauw en het cijfer "0" in zwart. Herhaal deze truc voor een groot aantal getallen om de toepassing van plaatswaarde op het bord te laten zien.
Deel 3 van 3: Gebruik interactieve voorbeelden
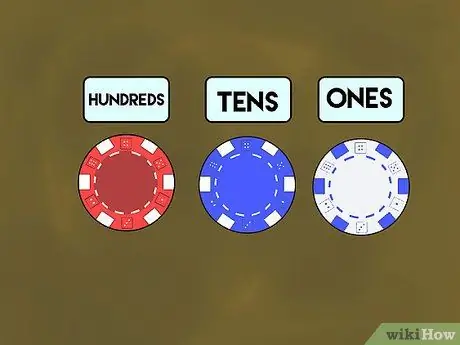
Stap 1. Geef les met pokerchips
Deel eerst de pokerfiches uit aan elke leerling. Vertel hen dat de witte fiches de "enen"-plaats vertegenwoordigen, de blauwe fiches voor "tientallen", en de rode fiches de "honderden". Laat uw leerlingen vervolgens zien hoe ze getallen kunnen maken met behulp van plaatswaarden in de vorm van kleurrijke chips. Noem een nummer (zeg 7) en plaats de witte chip rechts van je bureau.
- Noem een ander getal, bijvoorbeeld 30. Zet drie blauwe fiches die 3 vertegenwoordigen (op de plaats van de "tientallen") en nul witte fiches om 0 te vertegenwoordigen (op de plaats van de "enen").
- Je hoeft geen pokerchips te gebruiken. U kunt elk object gebruiken om de drie basis "plaats" -waarden weer te geven, zolang elke groep (chipkleur, enz.) Standaard, homogeen en gemakkelijk herkenbaar is.

Stap 2. Instrueer de leerlingen om stukken met elkaar uit te wisselen
Deze methode kan de lage plaatswaarden illustreren die de hogere plaatswaarden vormen. Zodra de leerlingen hebben aangetoond dat ze de waarde van een plaats goed begrijpen, leer je je klas hoe je witte "enen"-fiches kunt verwisselen voor blauwe "tientallen"-fiches en vervolgens "tientallen"-fiches ruilt voor "honderden". Vraag de leerlingen: "Hoeveel blauwe fiches krijg ik door 16 witte fiches in te wisselen? Als ik drie blauwe fiches ruil, hoeveel witte fiches krijg ik dan?"

Stap 3. Laat zien hoe je optellen en aftrekken doet met pokerchips
Dit concept kan alleen worden aangeleerd nadat studenten het uitwisselen van pokerchips onder de knie hebben. Het is handig om te beginnen met het schrijven van een voorbeeld.
- Vraag de leerlingen om voor het basisoptellingsprobleem drie blauwe fiches (tientallen) en zes witte fiches (enen) neer te leggen. Vraag de leerlingen naar de getallen die met de fiches zijn gevormd. (Het antwoord is 36!)
- Blijf werken aan hetzelfde nummer. Laat je leerlingen vijf witte fiches toevoegen aan het getal 36. Vraag hen naar het huidige getal. (Het antwoord is 41!) Neem vervolgens een blauwe chip en vraag hen het huidige nummer. (Het antwoord is 31!)






