- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:20.
- Laatst gewijzigd 2025-06-01 06:07.
Je zou kunnen denken dat gehele getallen gewone getallen zijn, zoals 3, -12, 17, 0, 7000 of -582. Gehele getallen worden ook wel gehele getallen genoemd omdat ze niet zijn verdeeld in delen zoals breuken en decimalen. Lees dit artikel om alles te leren over het optellen en aftrekken van gehele getallen, of lees direct de sectie die u nodig hebt.
Stap
Methode 1 van 5: Positieve gehele getallen optellen en aftrekken met behulp van een getallenlijn

Stap 1. Begrijp de getallenlijn
Cijferlijnen veranderen elementaire wiskunde in iets tastbaars en fysieks dat je kunt zien. Met slechts een paar tekens en gezond verstand kunnen we het gebruiken als een rekenmachine om getallen op te tellen en af te trekken.

Stap 2. Teken een basisgetallenlijn
Stel je voor of teken een even rechte lijn. Zet een punt in het midden van je lijn. Schrijven 0 of nul naast deze periode.
Je wiskundeboek zou dit het startpunt kunnen noemen, omdat het het startpunt is voor alle getallen

Stap 3. Teken twee stippen, één rechts en links van je nul
Schrijven - 1 naast de stip aan de linkerkant en
Stap 1. naast de stip aan de rechterkant. Dit is het gehele getal dat het dichtst bij nul ligt.
- Maak je geen zorgen over het maken van de afstanden tussen de punten precies hetzelfde - zolang je weet wat elk punt betekent, kan een getallenlijn worden gebruikt.
- De linkerkant is het begin van de zin.

Stap 4. Maak je getallenlijn af door meer getallen toe te voegen
Maak meer stippen naar links dan -1 en naar rechts dan 1. Aan de linkerkant, vanaf -1, markeer je stippen met - 2, - 3, en - 4. Aan de rechterkant, vanaf 1, markeer je punt met
Stap 2
Stap 3., da
Stap 4.. Je kunt doorgaan als je ruimte op je papier hebt.
Het voorbeeld in de afbeelding toont een getallenlijn van -6 tot 6

Stap 5. Begrijp wat positieve en negatieve gehele getallen zijn
Positieve gehele getallen, ook wel natuurlijk nummer, is een geheel getal groter dan nul. 1, 2, 3, 25, 99 en 2007 zijn positieve gehele getallen. Negatieve gehele getallen zijn gehele getallen die kleiner zijn dan nul (zoals -2, -4 en -88).
Gehele getallen zijn een andere manier om hele getallen te noemen. Breuken zoals 1/2 (half) zijn slechts een deel van het getal, dus het zijn geen gehele getallen. Hetzelfde als decimaal, bijvoorbeeld 0,25 (nul komma twee vijf); decimaal is geen geheel getal

Stap 6. Begin met het oplossen van 1+2 door je vinger op punt 1 te leggen
We zullen eenvoudige optelproblemen oplossen 1+2 met behulp van de getallenlijn die u zojuist hebt gemaakt. Het eerste nummer is
Stap 1., dus leg je vinger op het nummer.
-
Is deze vraag te makkelijk?
Als je ooit iets hebt toegevoegd, weet je waarschijnlijk het antwoord op 1+2. Goed: als je het resultaat kent, is het gemakkelijker om te begrijpen hoe de getallenlijn werkt. Vervolgens kun je de getallenlijn gebruiken om moeilijkere optelproblemen op te lossen of je voor te bereiden op moeilijkere wiskunde zoals algebra.

Stap 7. Tel 1+2 op door je vinger 2 puntjes naar rechts te bewegen
Schuif je vinger naar rechts en tel het aantal stippen (een ander getal) dat je passeert. Als je 2 nieuwe punten hebt gehaald, stop dan. Het nummer waar je vinger naar wijst is het antwoord,
Stap 3
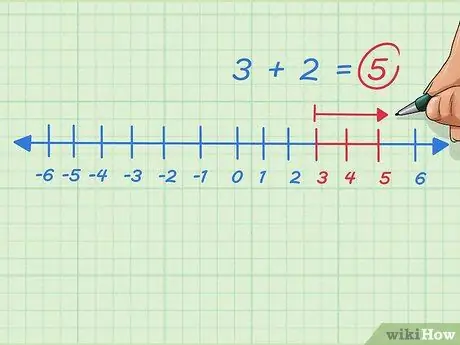
Stap 8. Voeg eventuele positieve gehele getallen toe door naar rechts op de getallenlijn te gaan
Stel dat we 3+2 willen oplossen. Begin bij 3, ga naar rechts of voeg 2 stippen toe. We stoppen bij 5. Het probleem is geschreven 3 + 2 = 5.

Stap 9. Trek positieve gehele getallen af door naar links op de getallenlijn te gaan
We willen bijvoorbeeld 6 -4 oplossen, we beginnen bij 6, gaan 4 punten naar links en stoppen bij 2. Dit probleem wordt geschreven 6 - 4 = 2.
Methode 2 van 5: Negatieve getallen optellen en aftrekken met een getallenlijn

Stap 1. Leer over getallenlijnen
Als u niet weet hoe u een getallenlijn moet maken, ga dan terug naar het gedeelte Positieve getallen optellen en aftrekken met behulp van getallenlijnen om te leren hoe u er een kunt maken.
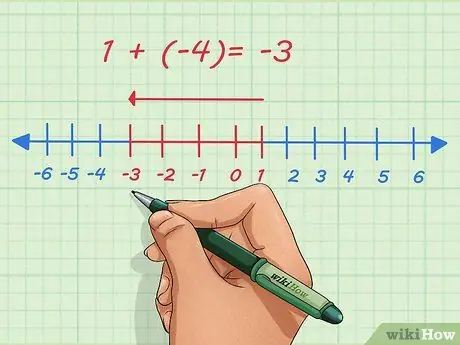
Stap 2. Begrijp wat negatieve getallen zijn
Positieve getallen worden aangegeven door de richting naar rechts op de getallenlijn. Negatieve getallen worden links op de getallenlijn aangegeven. Negatieve getallen toevoegen betekent het punt naar links op de getallenlijn verplaatsen.
-
Laten we bijvoorbeeld 1 en -4 optellen. Meestal wordt deze vraag als volgt geschreven:
1 + (-4)
. Op de getallenlijn beginnen we bij 1, schuiven 4 punten naar links en stoppen bij -3.
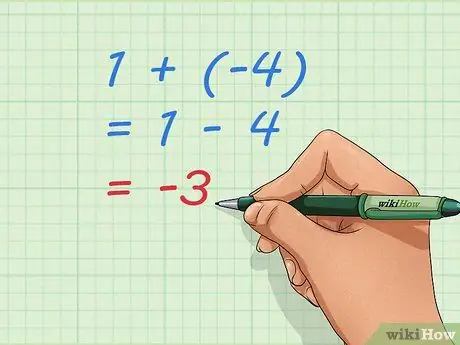
Stap 3. Gebruik basisvergelijkingen om het optellen van negatieve getallen te begrijpen
Merk op dat -3, ons antwoord, het getal is dat we krijgen als we 1 - 4 doen. Het optellen van 1 + (-4) en het aftrekken van 4 van 1 is hetzelfde probleem. We kunnen het schrijven als een vergelijking, een wiskundige zin die gelijkheid laat zien: 1 + (-4) = 1 - 4 = -3
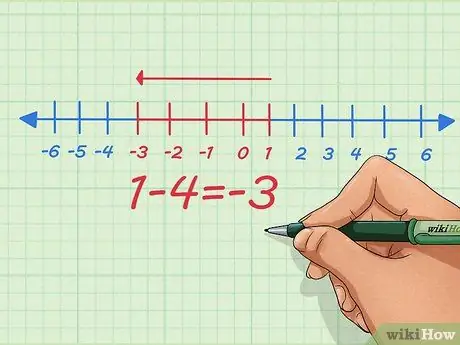
Stap 4. In plaats van negatieve getallen op te tellen, verander je het in een aftrekprobleem met positieve getallen
Zoals we kunnen zien aan de eenvoudige vergelijking hierboven, kunnen we beide doen - het optellen van negatieve getallen omzetten in aftrekking van positieve getallen en vice versa. Je hebt misschien geleerd om negatieven in negatieven te veranderen zonder te weten waarom - dit is waarom.
-
Bijvoorbeeld -4. Wanneer we -4 en 1 optellen, trekken we 1 af bij 4. Het kan in wiskunde worden geschreven door te schrijven
1 + (-4) = 1 - 4
. We kunnen dit op de getallenlijn schrijven, beginnend bij ons startpunt bij 1, en vervolgens 4 punten toevoegen aan de linkerkant (met andere woorden, -4 toevoegen). Aangezien dit een vergelijking is, is het ene gelijk aan het andere - dus het tegenovergestelde is ook waar
1 - 4 = 1 + (-4)
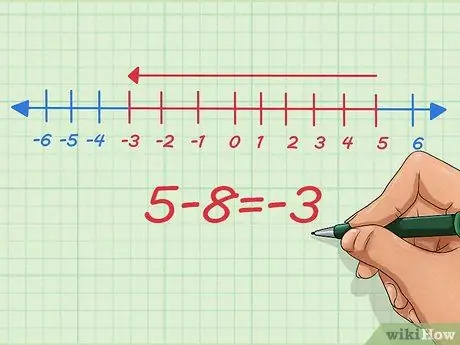
Stap 5. Begrijp hoe je negatieve getallen van een getallenlijn aftrekt
Op de getallenlijn is het aftrekken van negatieve getallen hetzelfde als het verkleinen van de lengte. Laten we beginnen met 5 - 8.
Op de getallenlijn beginnen we bij ons startpunt bij 5, trekken 8 af en stoppen bij -3
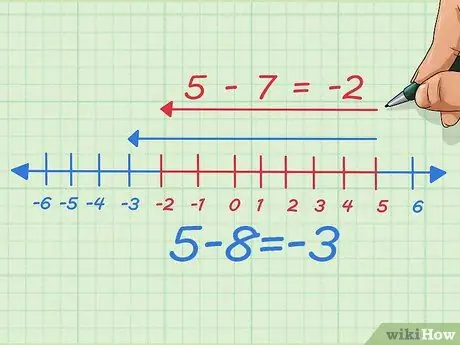
Stap 6. Trek het bedrag af dat u aftrekt en kijk wat er gebeurt
Stel dat we er één van aftrekken, het getal dat we aftrekken, of met andere woorden 7 aftrekken in plaats van 8. Nu trekken we één punt naar links op de getallenlijn af. Schriftelijk zijn we begonnen met 5 - 8 = -3 Nu gaan we 7 naar links, dus het wordt 5 - 7 = -2
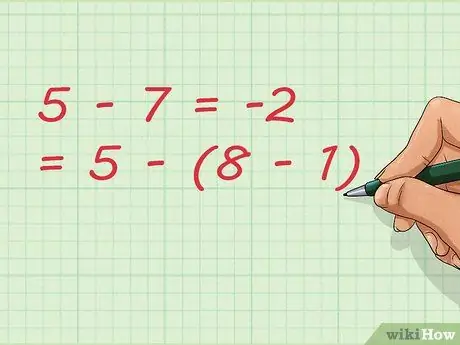
Stap 7. Merk op dat aftrekken kan resulteren in optellen
In ons voorbeeld trekken we het getal 1 af. Bij het schrijven van de vergelijking kunnen we deze korter schrijven, zoals: 5 - 7 = -2 = 5 - (8 - 1)

Stap 8. Zet negatieve tekens om in positief bij het toevoegen van negatieve getallen
Met behulp van de stap van het converteren van alle aftrekkingen naar optellingen, kunnen we kortere schrijven zoals: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
We weten al dat 5 - 8 = -3, dus haal 5 - 8 uit de vergelijking en voer -3 in:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
We weten al dat 5 - (8 - 1) is - één punt aftrekt van 5 - 8. Onze vergelijking kan aantonen dat 5 - 8 gelijk is aan -3, en één punt aftrekken geeft -2. De vergelijking kan als volgt worden geschreven:
-3 - (-1) = -3 + 1
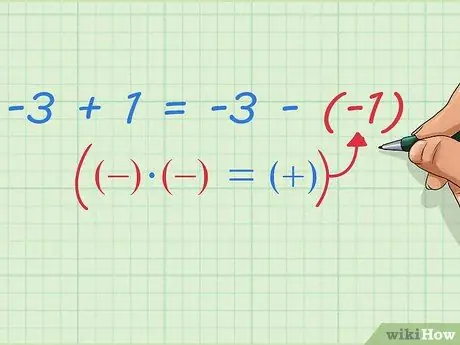
Stap 9. Schrijf de aftrekking van negatieve getallen als optelling
Merk op wat er hierna gebeurt - we hebben al bewezen dat: -3 + 1 = -3 - (-1) We kunnen dit schrijven met eenvoudigere en meer algemene rekenregels: eerste cijfer plus tweede cijfer = eerste cijfer min (negatief tweede cijfer) Of, een eenvoudigere manier die je waarschijnlijk hebt gehoord in de wiskundeles: Verander de twee negatieve tekens in een positief teken.
Methode 3 van 5: Positieve grote gehele getallen toevoegen

Stap 1. Schrijf het optelprobleem van 2.503 + 7.461 met het ene getal boven het andere
Noteer de getallen in de grote kolom zodat 2 meer is dan 7, 5 meer is dan 4, enzovoort. Op deze manier zullen we leren hoe we gehele getallen kunnen optellen die te groot zijn om de getallenlijn voor te stellen of te gebruiken.
Schrijf een +-teken links van het nummer eronder en de regel eronder, zoals je zou kunnen leren voor kleinere optelproblemen
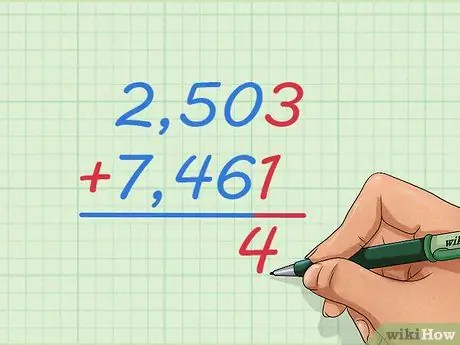
Stap 2. Begin met het optellen van de twee getallen uiterst rechts
Het is misschien een beetje vreemd om van rechts te beginnen, omdat we getallen van links lezen. We moeten van rechts toevoegen om het juiste antwoord te krijgen, wat je later kunt zien.
-
Onder de twee meest rechtse nummers,
Stap 3. da
Stap 1., schrijf de som van de twee op
Stap 4..

Stap 3. Tel elk getal in de kolom op dezelfde manier op
Naar links verplaatsen, optellen 0+6, 5+4, en 2+7. Schrijf het antwoord onder elk cijferpaar.
Uw antwoord zou moeten zijn: 9.964. Controleer je werk als je een fout maakt.

Stap 4. Tel nu 857+135 op
U zult iets anders opmerken zodra u het eerste paar getallen aan de rechterkant optelt. 7+5 is gelijk aan 12, een getal van twee cijfers, maar u kunt slechts één cijfer onder die kolom schrijven. Blijf lezen om erachter te komen wat je moet doen en waarom je altijd van rechts moet beginnen en niet van links.

Stap 5. Tel 7+5 bij elkaar op en leer waar je het antwoord moet schrijven
7+5=12, maar je kunt 1 en 2 niet onder de streep zetten. Maar, schrijf het laatste cijfer op, Stap 2., onder de streep en noteer het eerste cijfer
Stap 1., boven de kolom links, 5+3.
-
Als je nieuwsgierig bent naar hoe het werkt, denk dan eens na over wat het splitsen van 1 en 2 betekent. Je deelt 12 eigenlijk in
Stap 10. da
Stap 2.. Je kunt 10 boven het getal schrijven als je wilt, en je ziet 1 in kolom 5 en 3, net als voorheen.

Stap 6. Tel 1+5+3 op om het volgende cijfer van het antwoord te krijgen
Nu moet je drie cijfers optellen omdat je 1 aan deze kolom hebt toegevoegd. Het antwoord is
Stap 9., dus je antwoord wordt 92.
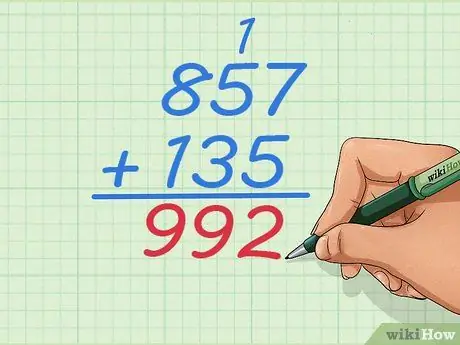
Stap 7. Voltooi het probleem zoals gewoonlijk
Blijf de cijfers naar links werken totdat je alle getallen hebt opgeteld, in dit geval is er nog maar één kolom over. Je laatste antwoord zou moeten zijn: 992.
- U kunt meer gecompliceerde vragen proberen, zoals 974+568. Onthoud dat wanneer u een getal van twee cijfers krijgt, u alleen het laatste cijfer als antwoord schrijft en het andere cijfer boven de kolom aan de linkerkant plaatst, die u vervolgens gaat optellen. Als het antwoord in de laatste kolom (uiterst links) twee cijfers bevat, noteer het dan als je antwoord.
- Zie het gedeelte Tips voor antwoorden op vragen 974+568 als je eenmaal hebt geprobeerd ze op te lossen.
Methode 4 van 5: Positieve grote gehele getallen aftrekken

Stap 1. Schrijf het aftrekprobleem 4.713 - 502 met het eerste getal boven het tweede getal
Schrijf het zo dat 3 direct boven 2 is, 1 boven 0, 7 boven 5 en 4 boven de blanco.
Je kunt 0 onder 4 schrijven als dit je helpt te onthouden welk getal boven welk getal staat. U kunt altijd een 0 voor een getal toevoegen zonder het te wijzigen. Zorg ervoor dat u het vóór het nummer toevoegt, niet erna

Stap 2. Trek elk getal eronder af van het getal er direct boven
Begin altijd van rechts. Los 3-2, 1-0, 7-5 en 4-0 op, schrijf het antwoord op elke vraag direct onder de twee afgetrokken getallen.
Het resultaat is, 4.211.

Stap 3. Schrijf nu vragen 924 - 518 op dezelfde manier
Deze nummers hebben hetzelfde aantal cijfers, dus u kunt ze gemakkelijk opschrijven. Dit probleem leert je iets over het aftrekken van gehele getallen als je het nog niet weet.

Stap 4. Leer hoe je het eerste probleem oplost, dat helemaal rechts staat
4 - 8. Dit probleem is ingewikkeld omdat 4 kleiner is dan 8, maar gebruik geen negatieve getallen, maar volg deze stappen:
- Kruis in de bovenste rij 2 aan en schrijf 1. 2 moet links van 4 staan.
- Kruis 4 aan en schrijf 14. Doe dit in een smalle ruimte zodat duidelijk is dat 14 meer is dan 8. Je kunt ook 1 voor 4 schrijven om 14 te maken als er genoeg ruimte is.
- Wat je zojuist hebt gedaan, is 1 lenen van de plaats van de tientallen of de tweede kolom van rechts en deze omrekenen naar 10 op de plaats van de enen of de kolom uiterst rechts. Zodra het getal 10 gelijk is aan tien keer het getal 1, is het hetzelfde.

Stap 5. Los nu de problemen 14 - 8 op en schrijf het antwoord onder de meest rechtse kolom
Er had 6 op de meest rechtse antwoordregel moeten staan.

Stap 6. Vul de volgende kolom aan de linkerkant in met het nieuwe nummer dat je hebt opgeschreven
De aftrekking moet 1 - 1 zijn, wat gelijk is aan 0.
Je antwoord zou nu moeten zijn: 06.

Stap 7. Los het probleem op door de laatste aftrekking, de meest linkse kolom, in te vullen
9 - 5 = 4, dus je uiteindelijke antwoord is 406.

Stap 8. Nu lossen we het probleem op van het aftrekken van grote getallen van kleine getallen
Stel dat u wordt gevraagd om 415.990 - 968.772 in te vullen. Schrijf het tweede getal onder het eerste getal en je zult je realiseren dat het onderstaande getal groter is! Aan het eerste cijfer links zie je meteen: 9 is groter dan 4, dus getallen die beginnen met 9 zijn groter.
Zorg ervoor dat u de kolom correct opschrijft voordat u gaat vergelijken. 912 Nee groter is dan 5000, kunt u zien of u de kolom correct schrijft, omdat er geen getallen onder 5 zijn. U kunt nulhulp toevoegen, bijvoorbeeld 912 schrijven met 0912 zodat de kolom gelijk is aan 5000.

Stap 9. Schrijf het kleinere getal onder het grotere getal en voeg een - teken toe voor het antwoord
Telkens wanneer u een getal van een kleiner getal aftrekt, is het resultaat een negatief getal. Het is beter om dit teken te schrijven voordat u het aftrekt, zodat u niet vergeet het op te schrijven.

Stap 10. Om te antwoorden, trekt u het kleine getal van het grote getal af en vergeet u niet het - teken te schrijven
Uw antwoord is negatief, wat wordt aangegeven met een - teken. Niet doen probeert een groot getal van een klein getal af te trekken en maakt het resultaat dan negatief; je antwoord zal fout zijn.
Het nieuwe op te lossen probleem is: 968.772 - 415.990 = -? Zie de sectie Tips voor het antwoord nadat u geprobeerd heeft dit probleem op te lossen
Methode 5 van 5: Negatieve gehele getallen optellen en aftrekken
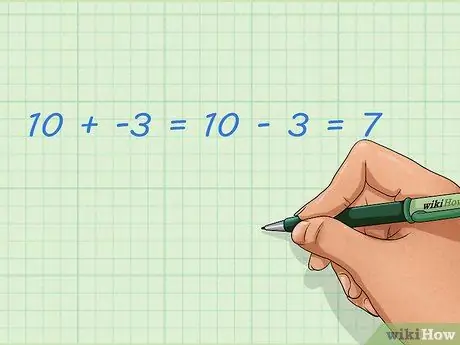
Stap 1. Leer hoe u negatieve en positieve getallen optelt
Het optellen van negatieve gehele getallen is hetzelfde als het aftrekken van positieve gehele getallen. Dit is gemakkelijker te doen met de getallenlijn die in een andere sectie wordt beschreven, maar je kunt het ook in woorden bedenken. Negatieve getallen zijn geen gewone getallen; dit aantal is kleiner dan nul en kan het genomen bedrag vertegenwoordigen. Als je deze take optelt bij een normaal getal, wordt het resultaat kleiner.
- Voorbeeld: 10 + -3 = 10 - 3 = 7
- Voorbeeld: -12 + 18 = 18 + -12 = 18 - 12 = 6. Onthoud dat je de volgorde van getallen altijd kunt wijzigen bij optellen, maar niet bij aftrekken.
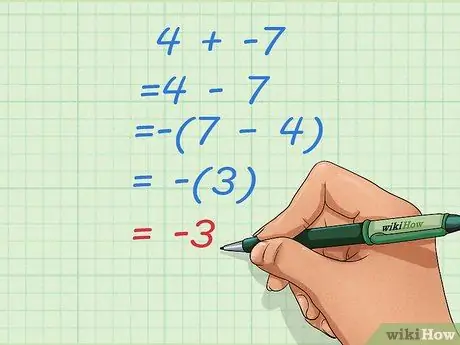
Stap 2. Leer wat je moet doen als je er een aftrekprobleem van maakt met een kleiner startgetal
Soms kan het veranderen van optellen bij aftrekken, zoals hierboven, leiden tot vreemde antwoorden zoals 4 - 7. Als dit gebeurt, keert u de volgorde van de getallen om en maakt u uw resultaat negatief.
- Laten we zeggen dat uw eerste probleem 4 + -7 is.
- Verander het in een aftrekprobleem: 4 - 7
- Keer de volgorde om en maak het resultaat negatief: -(7 - 4) = -(3) = -3.
- Als je niet bekend bent met het gebruik van haakjes in vergelijkingen, denk hier dan eens over na: 4 - 7 wordt 7 - 4 met de toevoeging van een minteken. 7 - 4 = 3, maar we moeten het veranderen in -3 zodat het antwoord op de vragen 4 - 7 correct is.
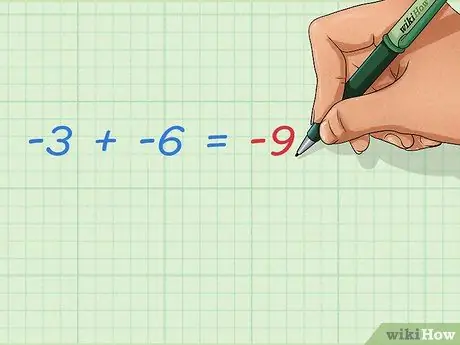
Stap 3. Leer hoe u twee negatieve gehele getallen kunt optellen
Twee opgetelde negatieve getallen maken het negatieve resultaat altijd groter. Aangezien er geen positieve getallen worden toegevoegd, zal het resultaat verder van 0 af liggen. Het antwoord is eenvoudig:
- -3 + -6 = -9
- -15 + -5 = -20
- Zie je het patroon? Het enige dat u hoeft te doen, is de getallen optellen alsof het positieve getallen zijn en een negatief teken toevoegen. -4 + -3 = -(4 + 3) = -7
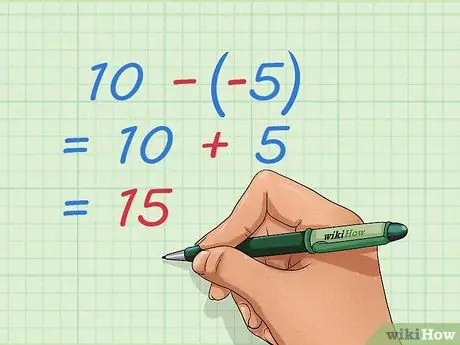
Stap 4. Leer hoe u negatieve gehele getallen kunt aftrekken
Net als het optelprobleem, kun je het probleem herschrijven zodat je alleen positieve getallen hebt. Als je negatieve getallen aftrekt, haal je een deel van de dingen weg die al zijn genomen, wat hetzelfde is als positieve getallen optellen.
- Denk aan negatieve getallen als gestolen geld. Als je gestolen geld aftrekt of wegneemt zodat je het terug kunt geven, is het alsof je geld aan iemand geeft, toch?
- Voorbeeld: 10 - -5 = 10 + 5 = 15
- Voorbeeld: -1 - -2 = -1 + 2. Je hebt al in de eerste stap geleerd hoe je dit probleem kunt oplossen, weet je nog? Lees opnieuw hoe u negatieve en positieve getallen toevoegt als u het bent vergeten.
- Hier is de volledige oplossing van het laatste voorbeeld: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Tips
- Je hebt misschien lange getallen zoals 2.521.301 geschreven met komma's (,) in plaats van (.), afhankelijk van waar je woont. Gebruik wat je leraar je vraagt, zodat je niet in de war raakt met andere schrijfsystemen.
- Teken uw getallenlijnen op verschillende schalen om verschillende getallen weer te geven. Er is geen regel dat elke afstand op een getallenlijn gelijk is aan 1. Stel je een getallenlijn voor die 10 is in plaats van 1. Afgezien van het feit dat elk punt nu 10 is, blijven optellen en aftrekken hetzelfde. Probeer het als je het niet gelooft.
- Als je de speciale uitdagingsvragen in het gedeelte Lange getallen probeert, is dit het antwoord: 974 + 568 = 1.542. Het antwoord van 415.990 - 968.772 is - 552.782.






