Breuken delen door hele getallen is niet zo moeilijk als het lijkt. Om een breuk te delen door een geheel getal, hoef je alleen maar het hele getal om te zetten in een breuk, het omgekeerde van de breuk te vinden en het resultaat te vermenigvuldigen met de eerste breuk. Als u wilt weten hoe u dit moet doen, volgt u deze stappen:
Stap
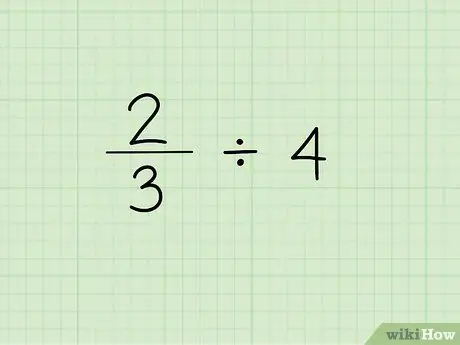
Stap 1. Schrijf het probleem op
De eerste stap om een breuk te delen door een geheel getal is om de breuk te schrijven gevolgd door het deelteken en het gehele getal dat je nodig hebt om de breuk te delen. Laten we zeggen dat we met het volgende probleem werken: 2/3 4.
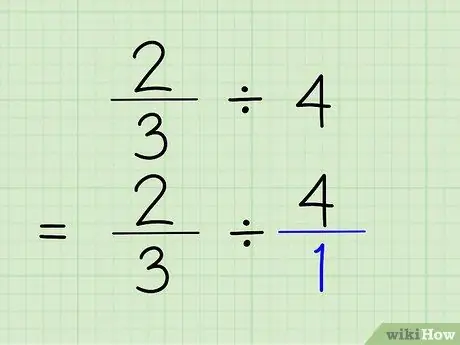
Stap 2. Converteer gehele getallen naar breuken
Om een geheel getal om te zetten in een breuk, hoeft u alleen het gehele getal boven het getal 1 te plaatsen. Het geheel getal wordt de teller en 1 wordt de noemer van de breuk. 4/1 zeggen is eigenlijk hetzelfde als 4 zeggen, omdat je alleen laat zien dat het getal 4 keer "1" bevat. Het probleem zal 2/3 4/1 zijn.
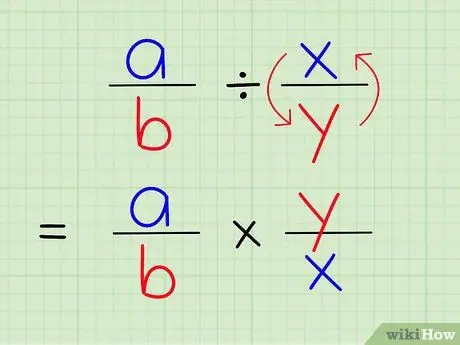
Stap 3. Een breuk delen door een andere is hetzelfde als die breuk vermenigvuldigen met het omgekeerde van een andere breuk
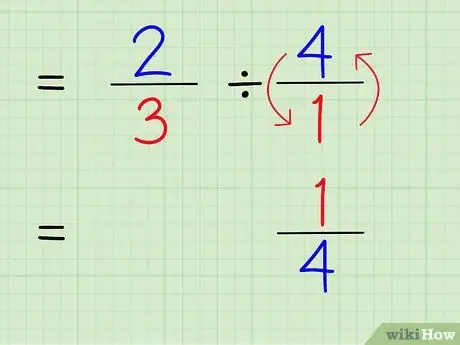
Stap 4. Schrijf het omgekeerde van het gehele getal
Om het omgekeerde van een getal te vinden, verwissel je de teller en noemer van het getal. Daarom, om het omgekeerde van 4/1 te vinden, verwisselt u eenvoudig de teller en de noemer zodat het getal 1/4 wordt.
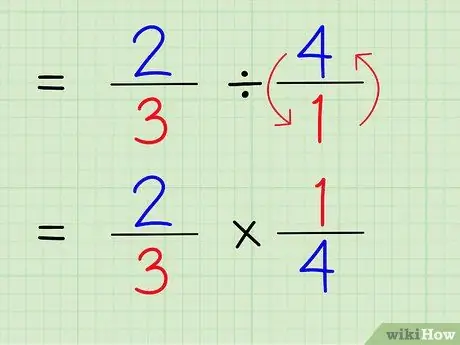
Stap 5. Verander het deelteken in het vermenigvuldigingsteken
Het probleem zal 2/3 x 1/4 zijn.
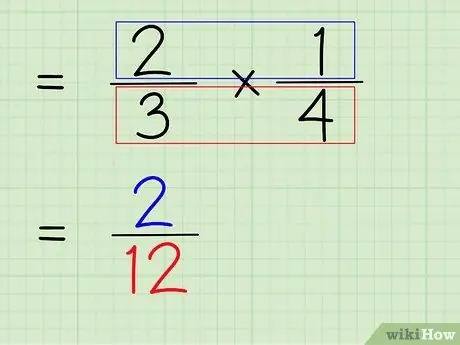
Stap 6. Vermenigvuldig de teller en noemer van de breuk
Dus de volgende stap is om de teller en noemer van de breuk te vermenigvuldigen om een nieuwe teller en noemer als het laatste antwoord te krijgen.
- Om de tellers te vermenigvuldigen, vermenigvuldig je gewoon 2 x 1 om 2 te krijgen.
- Om de noemers te vermenigvuldigen, vermenigvuldig je gewoon 3 x 4 om 12 te krijgen.
- 2/3 x 1/4 = 2/12
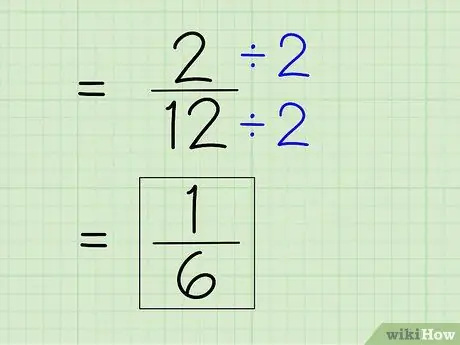
Stap 7. Vereenvoudig de breuk
Om een breuk te vereenvoudigen, moet je de kleinste noemer vinden, wat betekent dat je de teller en de noemer moet delen door een willekeurig getal dat beide getallen deelt. Omdat 2 de teller is, moet je kijken of 2 12 volledig kan delen - dat kan omdat 12 een even getal is. Deel vervolgens de teller en noemer door 2 om een nieuwe teller en noemer te krijgen om een eenvoudig antwoord te krijgen.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- De breuk 2/12 kan worden vereenvoudigd tot 1/6. Dit is uw laatste antwoord.
Tips
- Dit is ter ondersteuning van het geheugen, een gemakkelijke manier om te onthouden hoe u al deze berekeningen moet uitvoeren. Houd dit in gedachten: "Het is gemakkelijk om breuken te delen, het tweede getal om te keren en te vermenigvuldigen!"
- Een andere variant van de bovenstaande methode is JGB/JBG. Verander het eerste nummer niet. Verander in vermenigvuldiging. Draai het laatste nummer om. Of eerst B en dan G.
- Als u de berekening annuleert voordat u deze vermenigvuldigt, hoeft u misschien niet de eenvoudigste vorm van de breuk te vinden, omdat het resultaat al in de eenvoudigste breukvorm staat, zoals u kunt zien. In ons voorbeeld, voordat we 2/3 × 1/4 vermenigvuldigen, kunnen we zien dat de eerste teller (2) en de tweede noemer (4) dezelfde vermenigvuldiger van 2 hebben, die we kunnen annuleren voordat we verder gaan met de berekening. Dit converteert het probleem naar 1/3 × 1/2, wat een onmiddellijk 1/6 resultaat geeft en ons tijd bespaart om de breuk in een later stadium te vereenvoudigen.
- Als een van je breuken negatief is, is deze methode nog steeds werkbaar; zorg ervoor dat u de tekens bijhoudt terwijl u deze stappen uitvoert.
