- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:20.
- Laatst gewijzigd 2025-01-23 12:42.
Een breuk delen door een breuk lijkt in eerste instantie misschien verwarrend, maar het is eigenlijk heel eenvoudig. Het enige wat u hoeft te doen is omdraaien, vermenigvuldigen en vereenvoudigen! Dit artikel leidt u door het proces en laat u zien hoe gemakkelijk het is om een breuk door een breuk te delen.
Stap
Deel 1 van 2: Begrijpen hoe breuken te delen door breuken
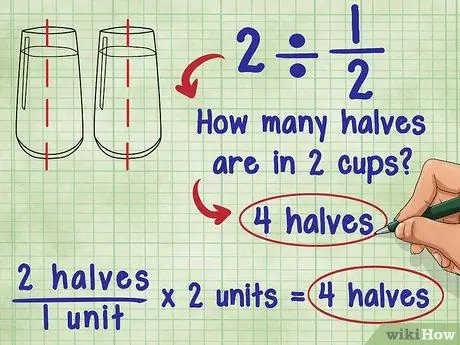
Stap 1. Bedenk wat delen door een breuk betekent
Wat betreft 2 ÷ 1/2 vroeg Ada: "Hoeveel helften zijn er in 2?" Het antwoord is 4 omdat elke eenheid (1) uit twee "helften" bestaat en er in totaal 2 eenheden zijn: 2 "halve"/1 eenheid * 2 eenheden = 4 "halve".
- Probeer je dezelfde vergelijking voor te stellen met een glas water: hoeveel en een half glas water zitten in 2 glazen water? U kunt 2 en een half kopje water in elk glas water gieten. Dat betekent in feite dat je de "halve" glazen water bij elkaar optelt en je hebt twee glazen: 2 "halve"/1 kop * 2 kopjes = 4 "halve".
- Dit betekent dat als de breuk die je deelt tussen 0 en 1 ligt, het antwoord altijd groter is dan het oorspronkelijke getal! Dit is het geval wanneer u een geheel getal of een breuk deelt door een breuk.

Stap 2. Begrijp dat delen het tegenovergestelde is van vermenigvuldigen
Dus delen door een breuk kan worden opgelost door te vermenigvuldigen met het omgekeerde van de breuk. Het omgekeerde van een breuk (ook wel de “inverse vermenigvuldiging” genoemd) is de breuk die wordt omgekeerd, zodat de teller en noemer van plaats wisselen. Zo meteen delen we breuken door breuken, door de reciproke van de tweede breuk te vinden en beide breuken te vermenigvuldigen. Laten we echter eerst naar enkele van de tegenstellingen kijken:
- Het omgekeerde van 3/4 is 4/3.
- Het tegenovergestelde van 7/5 is 5/7.
- Het omgekeerde van 1/2 is 2/1 of 2.
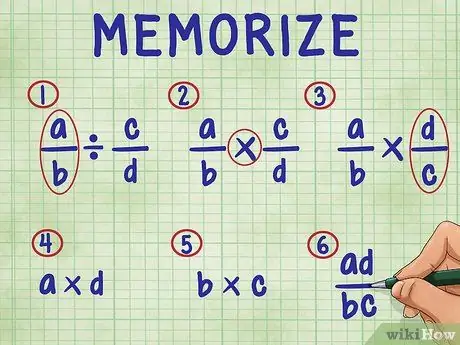
Stap 3. Onthoud de volgende stappen om een breuk door een breuk te delen
In volgorde omvatten de stappen:
- Laat gewoon de eerste breuk in de vergelijking.
- Verander het deelteken in het vermenigvuldigingsteken.
- Keer de tweede breuk om (vind de reciproke).
- Vermenigvuldig de teller (bovenste getal) van beide breuken. Het resultaat van de vermenigvuldiging is de teller (bovenaan) van je antwoord.
- Vermenigvuldig de noemer (onderste getal) van beide breuken. Het product van het product is de noemer van je antwoord.
- Vereenvoudig uw breuken door ze te vereenvoudigen tot hun eenvoudigste termen.
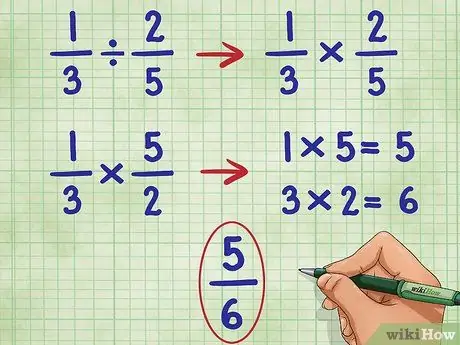
Stap 4. Voer deze stappen uit voor het voorbeeld 1/3 2/5
We beginnen met het weglaten van de eerste breuk en het omzetten van het deelteken naar het vermenigvuldigingsteken:
- 1/3 ÷ 2/5 = Wordt:
- 1/3 * _ =
- Nu keren we de tweede breuk (2/5) om om de reciproke te vinden, die 5/2 is:
- 1/3 * 5/2 =
- Vermenigvuldig nu de teller (topgetal) van beide breuken, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Vermenigvuldig nu de noemer (onderste getal) van beide breuken, 3*2 = 6.
- Nu hebben we: 1/3 * 5/2 = 5/6
- Deze breuk kan niet verder worden vereenvoudigd, dus we hebben ons antwoord.

Stap 5. Probeer de volgende rijmpjes te onthouden om je te helpen herinneren:
"Fracties delen is eenvoudig, keer de tweede breuk om en vermenigvuldig dan. Vergeet niet te vereenvoudigen, voordat het tijd is om te eten."
Een andere handige herinnering vertelt u wat u met elk deel van de vergelijking moet doen: "Laat mij (eerste breuk), verander mij (deelteken), keer mij om (tweede breuk)."
Deel 2 van 2: Breuken delen door breuken in problemen
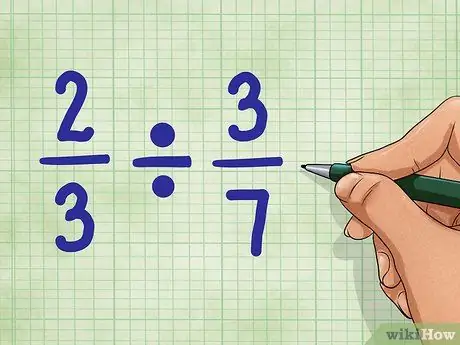
Stap 1. Begin met voorbeeldvragen
Laten we gebruiken 2/3 ÷ 3/7. Deze vraag vraagt om het aantal delen gelijk aan 3/7, te vinden in de waarde 2/3. Maak je geen zorgen. Het is niet zo moeilijk als het klinkt!
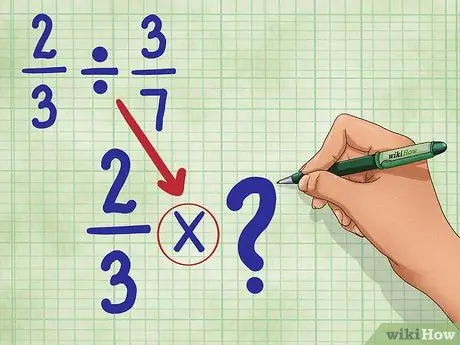
Stap 2. Converteer het deelteken naar het vermenigvuldigingsteken
Je nieuwe vergelijking wordt: 2/3 * _ (We vullen deze blanco zo meteen in.)
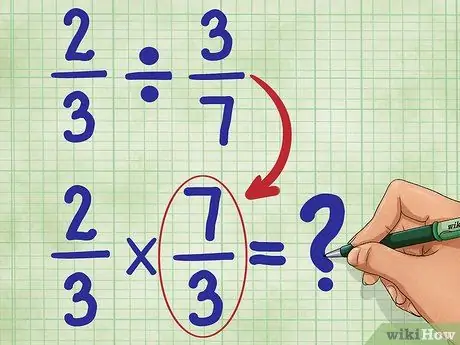
Stap 3. Zoek nu het omgekeerde van de tweede breuk
Dit betekent 3/7 omdraaien zodat de teller (3) nu onderaan staat en de noemer (7) nu bovenaan. Het omgekeerde van 3/7 is 7/3. Schrijf nu je nieuwe vergelijking:
2/3 * 7/3 = _

Stap 4. Vermenigvuldig je breuken
Vermenigvuldig eerst de tellers van beide breuken: 2 * 7 = 14. 14 is de teller (bovenste getal) van je antwoord. Vermenigvuldig vervolgens de noemers van beide breuken: 3 * 3 = 9. 9 is de noemer (onderste getal) van je antwoord. Nu weet je dat 2/3 * 7/3 = 14/9.
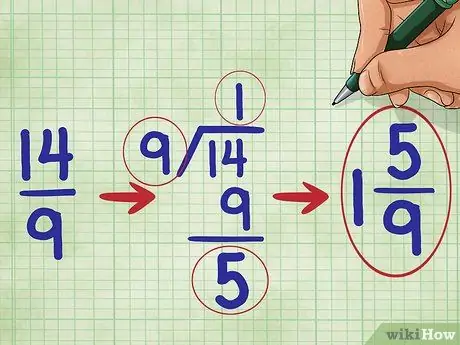
Stap 5. Vereenvoudig je breuk
In dit probleem, omdat de teller van de breuk groter is dan de noemer, weten we dat onze breuk groter is dan 1. We moeten het omrekenen naar een gemengd getal. (Een gemengd getal is een geheel getal en een breuk gecombineerd, bijvoorbeeld 1 2/3.))
-
Deel eerst de teller
Stap 14. met 9.
Het getal 14 gedeeld door 9 is gelijk aan één met een rest van 5, dus je moet je vereenvoudigde breuk opschrijven als: 1 5/9 (“een vijf-negende”).
- Stop, je hebt het antwoord gevonden! Je kunt aangeven dat je de breuk niet meer kunt vereenvoudigen omdat de noemer niet deelbaar is door de teller (9 is niet deelbaar door 5) en de teller een priemgetal is, of een geheel getal dat alleen deelbaar is door één en het getal zelf.
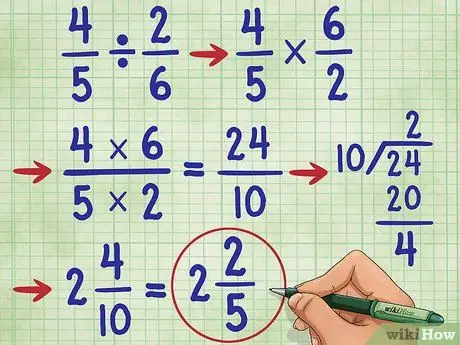
Stap 6. Probeer een ander voorbeeld
Laten we de vraag proberen 4/5 ÷ 2/6 =. Verander eerst het deelteken in het vermenigvuldigingsteken (4/5 * _ =), zoek dan het omgekeerde van 2/6, wat 6/2 is. Nu heb je de vergelijking: 4/5 * 6/2 =_. Vermenigvuldig nu de teller, 4 * 6 = 24, en de noemer 5* 2 = 10. Nu heb je 4/5 * 6/2 = 24/10.
Vereenvoudig nu de breuk. Aangezien de teller groter is dan de noemer, moeten we deze breuk omzetten in een gemengd getal.
- Deel eerst de teller door de noemer, (24/10 = 2 resterende 4).
- Schrijf het antwoord als 2 4/10. We kunnen deze breuk nog steeds vereenvoudigen!
- Merk op dat 4 en 10 even getallen zijn. Dus de eerste stap om het te vereenvoudigen is om elk getal door 2 te delen. We krijgen 2/5.
- Aangezien de noemer (5) niet deelbaar is door de teller (2) en 5 een priemgetal is, weten we dat deze breuk niet verder vereenvoudigd kan worden. Ons antwoord is dus: 2 2/5.

Stap 7. Krijg extra hulp bij het vereenvoudigen van breuken
Je hebt waarschijnlijk veel tijd besteed aan het leren hoe je breuken kunt vereenvoudigen voordat je ze door elkaar probeert te delen. Als u echter een opfriscursus of andere hulp nodig heeft, zijn er enkele geweldige online artikelen die u enorm kunnen helpen.
Gerelateerde wikiHow-artikelen
- Gewone breuken converteren naar decimalen
- De oppervlakte van een cirkel berekenen
- Polynomen delen met behulp van synthetische deling
- Gemengde breuken delen






