Lensvergroting berekenen: 12 stappen (met afbeeldingen)

2024 Auteur: Jason Gerald | [email protected]. Laatst gewijzigd: 2024-01-16 19:48

Bij het bestuderen van optische instrumenten is de "vergroting" van een lensachtig object de verhouding tussen de hoogte van het beeld dat je ziet en de werkelijke hoogte van het object. Een lens die een object bijvoorbeeld erg groot kan laten lijken, heeft een "hoge" vergrotingsfactor, terwijl een lens die een object klein doet lijken een "lage" vergrotingsfactor heeft. De formule voor de vergroting van een object wordt meestal berekend met de formule M = (h_l/H_O) = -(d_l/NS_O), waarbij M = vergroting, h_l = hoogte van afbeelding, h_O = hoogte van object, en d_l en D_O = afstand van beeld en object.

Stap

Methode 1 van 2: De vergroting van één lens berekenen

Opmerkingen: A convergerende lens breder in het midden dan aan de randen (zoals een vergrootglas). een divergente lens breder aan de randen dan in het midden (zoals een kom). Het berekenen van de vergroting op beide lenzen is hetzelfde, met een belangrijke uitzondering:. Klik hier om direct naar de uitzonderingen op afwijkende lenzen te gaan.

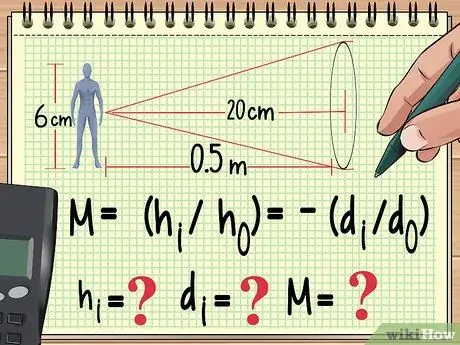
Stap 1. Begin met je vergelijking en de variabelen die je al kent

Net als elk ander natuurkundig probleem, kun je een vergrotingsprobleem oplossen door de vergelijking op te schrijven die je gaat gebruiken om het te berekenen. Vanaf hier kunt u achteruit werken om de waarde te vinden van de variabele die u niet hebt gevonden in de vergelijking die u gebruikt.

• Stel bijvoorbeeld dat een pop van 6 cm hoog op een meter afstand van een convergerende lens met een brandpuntsafstand van 20 cm. Als we de vergroting, beeldhoogte en beeldafstand willen berekenen, kunnen we onze vergelijking als volgt beginnen te schrijven:

  M = (h_l/H_O) = -(d_l/NS_O)

• Nu weten we h_O (hoogte van de pop) en d_O (pop afstand van lens). We kennen ook de brandpuntsafstand van de lens, die niet in deze vergelijking staat. We zullen tellen H_l, NS_l, en M.

Stap 2. De lensvergelijking gebruiken om d. te krijgen_l.

Als u de afstand tot het object dat u vergroot en de brandpuntsafstand van de lens kent, is het berekenen van de afstand tot het gevormde beeld heel eenvoudig met de lensvergelijking. De vergelijking van de lens is 1/f = 1/d_O + 1/d_l, waarbij f = brandpuntsafstand van de lens.

• In dit voorbeeldprobleem kunnen we de lensvergelijking gebruiken om d. te berekenen_l. Voer de waarden van f en d. in_l los dan de vergelijking op:

  1/f = 1/d_O + 1/d_l

  1/20 = 1/50 + 1/d_l

  5/100 - 2/100 = 1/d_l

  3/100 = 1/d_l

  100/3 = d_l = 33,3 cm

• De brandpuntsafstand van de lens is de afstand van het centrum van de lens tot het punt waar licht wordt doorgelaten op het brandpunt. Als je ooit licht met een vergrootglas hebt gericht op brandende mieren, dan heb je het gezien. Bij de vragen in de les is meestal de omvang van deze hotspot gegeven. In het echte leven staan deze specificaties meestal op een label op de lens.

Stap 3. H. berekenen_l.

Nadat je d. hebt berekend_O en D_l, kunt u de hoogte van het uitvergrote object en de vergroting van de lens berekenen. Let op de twee gelijktekens in de lensvergrotingsvergelijking (M = (h_l/H_O) = -(d_l/NS_O)) - dit betekent dat alle delen van deze vergelijking aan elkaar gelijk zijn, dus we kunnen M en h. berekenen_l in welke volgorde we willen.

• Voor dit voorbeeldprobleem kunnen we h. berekenen_l zoals dit:

  (H_l/H_O) = -(d_l/NS_O)

  (H_l/6) = -(33, 3/50)

  H_l = -(33, 3/50) x 6

  H_l = - 3, 996 cm

• Merk op dat de hoogte van het object hier negatief is, wat aangeeft dat het beeld dat we later zullen zien, zal worden omgekeerd (boven-onder).

Stap 4. Berekening van M

Je kunt de laatste variabele berekenen met de vergelijking -(d_l/NS_O) of (h_l/H_O).

• In het volgende voorbeeld is het berekenen van M als volgt:

  M = (h_l/H_O)

  M = (-3, 996/6) = - 0, 666

• Het resultaat is ook hetzelfde als het wordt berekend met de waarde van d:

  M = -(d_l/NS_O)

  M = -(33, 3/50) = - 0, 666

• Merk op dat de zoom geen eenheidslabel heeft.

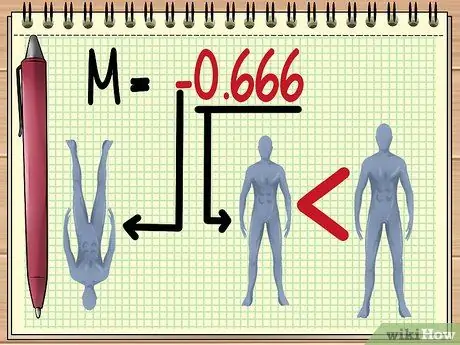
Stap 5. De M-waarde begrijpen

Zodra je de grootte van de M-waarde hebt, kun je verschillende dingen inschatten over het beeld dat je door de lens zult zien, namelijk:

• De grootte.

  Hoe groter de "absolute waarde" van M, hoe groter het met de lens bekeken object zal lijken. Een M-waarde tussen 0 en 1 geeft aan dat het object er kleiner uit zal zien.

• Objectoriëntatie.

  Een negatieve waarde geeft aan dat het gevormde beeld wordt omgekeerd.

• In het hier gegeven voorbeeld betekent de M-waarde van -0.666 dat, volgens de waarde van de bestaande variabele, de schaduw van de pop zichtbaar zal zijn. ondersteboven en tweederde kleiner dan de werkelijke grootte.

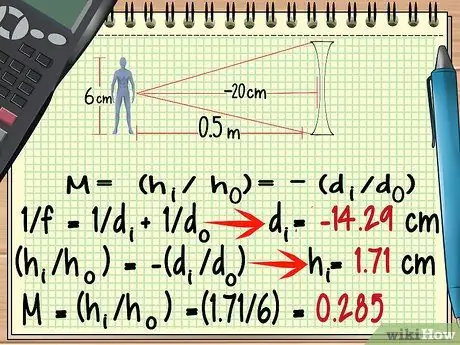
Stap 6. Gebruik voor een divergerende lens een negatief brandpunt

Hoewel de vorm van een divergerende lens heel anders is dan die van een convergerende lens, kun je de vergroting ervan berekenen met dezelfde formule als hierboven. De uitzonderingen om in gedachten te houden zijn: Het brandpunt van de divergerende lens is negatief.

In het bovenstaande voorbeeldprobleem heeft dit invloed op het antwoord dat u krijgt bij het berekenen van d_l, let hier dus goed op.

• Laten we het bovenstaande voorbeeldprobleem herwerken, alleen gebruiken we nu een divergerende lens met brandpuntsafstand - 20cm.

  De andere variabelen blijven dezelfde waarde.

• Allereerst berekenen we d_l met behulp van de lensvergelijking:

  1/f = 1/d_O + 1/d_l

  1/-20 = 1/50 + 1/d_l

  -5/100 - 2/100 = 1/d_l

  -7/100 = 1/d_l

  -100/7 = d_l = - 14, 29 cm

• Nu berekenen we h_l en M met een waarde van d_l de nieuwe.

  (H_l/H_O) = -(d_l/NS_O)

  (H_l/6) = -(-14, 29/50)

  H_l = -(-14, 29/50) x 6

  H_l = 1, 71 cm

  M = (h_l/H_O)

  M = (1, 71/6) = 0, 285

Methode 2 van 2: De vergroting van meerdere lenzen berekenen

Eenvoudige methode met twee lenzen

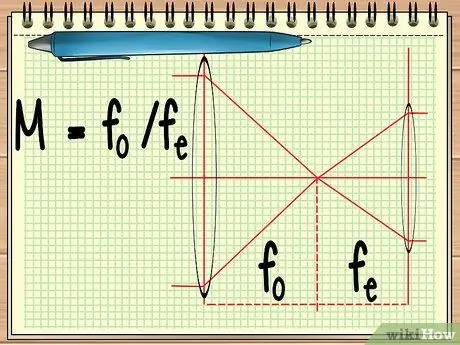
Stap 1. Bereken het brandpunt van de twee lenzen

Wanneer u een instrument gebruikt dat bestaat uit twee naast elkaar geplaatste lenzen (zoals een telescoop of een verrekijker), hoeft u alleen het brandpunt van de twee lenzen te vinden om de totale vergroting van de twee lenzen te berekenen. dit kan worden berekend door de eenvoudige vergelijking M = f_O/F_e.

In de vergelijking, f_O is het brandpunt van de objectieflens en f_e is het brandpunt van het oculair. De objectieflens is de grote lens die zich dicht bij het object bevindt, terwijl de oculaire lens de lens is die zich dicht bij het oog van de waarnemer bevindt.

Stap 2. Vul de informatie die je al hebt in de vergelijking M = f. in_O/F_e.

Als je eenmaal de brandpunten van beide lenzen hebt, is het heel eenvoudig om ze te berekenen, - bereken de verhouding door de brandpuntsafstand van de objectieflens te delen door de brandpuntsafstand van het oculair. Het antwoord dat u krijgt is de totale vergroting van de tool.

• Stel bijvoorbeeld een eenvoudige telescoop, er staat geschreven dat het brandpunt van de objectieflens 10 cm is en het brandpunt van het oculair is 5 cm, dan is de vergroting 10/5 = 2.

Ingewikkelde methode

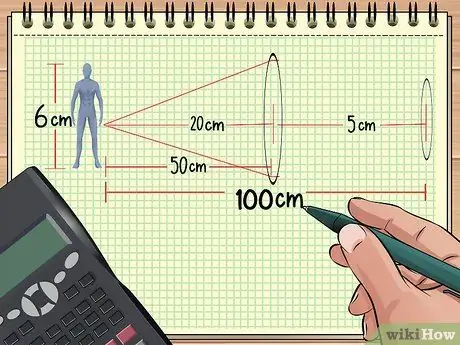
Stap 1. Bereken de afstand tussen de lenzen en het object

Als u twee lenzen in een rij voor een object hebt geplaatst, kan de totale vergroting worden berekend als u de afstand van de lenzen tot het object, de grootte van het object en het brandpunt van de twee lenzen kent. De rest kan ook worden berekend.

Stel dat we objecten en lenzen rangschikken zoals in het voorbeeldprobleem 1 hierboven: een pop staat op 50 cm van een convergerende lens met een brandpuntsafstand van 20 cm. Plaats nu de tweede lens met brandpunt 5 cm op een afstand van 50 cm van de eerste lens (100 cm van de pop). Daarna berekenen we de totale vergroting met de verkregen informatie

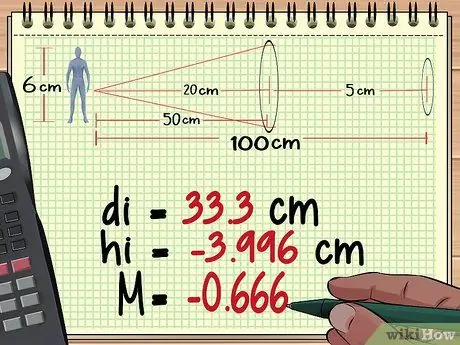
Stap 2. Bereken de objectafstand, hoogte en vergroting van lens 1

Het eerste deel van het berekenen van de vergroting van meerdere lenzen is hetzelfde als het berekenen van de vergroting van een enkele lens. Begin met de lens die zich het dichtst bij het object bevindt, gebruik de lensvergelijking om de afstand tot het gevormde beeld te vinden en gebruik vervolgens de vergrotingsvergelijking om de hoogte en vergroting van het beeld te vinden. Klik hier om meer berekeningen voor de vergroting van één lens te bekijken.

• Uit onze berekeningen in methode 1 hierboven blijkt dat de eerste lens een beeld produceert dat zo hoog is als - 3, 996 cm, afstand 33,3 cm achter de lens, en bij een vergroting van - 0, 666.

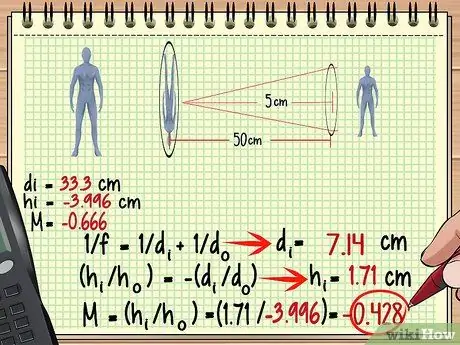
Stap 3. Gebruik het beeld van de eerste lens als het object van de tweede lens

Nu is het heel eenvoudig om de vergroting, hoogte en meer voor de tweede lens te vinden - gebruik gewoon dezelfde methode als voor de eerste lens, maar behandel het beeld deze keer als een object. Bedenk dat de beeldafstand tot de tweede lens niet altijd gelijk is aan de objectafstand tot de eerste lens.

• In het bovenstaande voorbeeld, aangezien het beeld 33,3 cm achter de eerste lens wordt gevormd, is de afstand 50-33,3 = 16,7 cm voor de tweede lens. Laten we deze meting en de brandpuntsafstand van de tweede lens gebruiken om het beeld te vinden dat door de tweede lens wordt gevormd.

  1/f = 1/d_O + 1/d_l

  1/5 = 1/16, 7 + 1/d_l

  0, 2 - 0, 0599 = 1/d_l

  0, 14 = 1/d_l

  NS_l = 7, 14 cm

• Nu kunnen we h. berekenen_l en M voor de tweede lens:

  (H_l/H_O) = -(d_l/NS_O)

  (H_l/-3, 996) = -(7, 14/16, 7)

  H_l = -(0, 427) x -3, 996

  H_l = 1, 71 cm

  M = (h_l/H_O)

  M = (1, 71/-3, 996) = - 0, 428

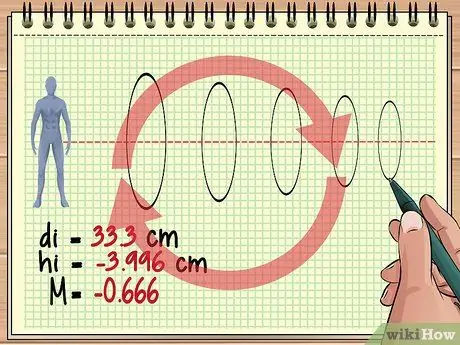
Stap 4. Ga zo verder met rekenen voor de extra lenzen

Deze basisbenadering is hetzelfde als er drie, vier of honderden lenzen voor een object zijn opgesteld. Beschouw voor elke lens het beeld van de vorige lens als het object en gebruik de lensvergelijking en de vergrotingsvergelijking om het gewenste antwoord te vinden.

Houd er rekening mee dat elke volgende lens het gevormde beeld continu kan omkeren. De vergrotingswaarde die we eerder hebben verkregen (-0, 428) geeft bijvoorbeeld aan dat het beeld dat we gaan zien ongeveer 4/10 van de werkelijke objectgrootte is, maar loodrecht, omdat het beeld van de vorige lens omgekeerd is

Tips

• Een verrekijker geeft meestal uitleg over de vergrotingsspecificaties in de vorm van een aantal maal een ander getal. Een verrekijker kan bijvoorbeeld worden gespecificeerd als 8x25 of 8x40. Als je het zo schrijft, is het eerste getal de vergroting van de verrekijker. Het maakt niet uit of in het gegeven voorbeeld de twee getallen verschillend van grootte zijn, beide verrekijkers hebben een vergroting van 8 keer. Het tweede cijfer geeft aan hoe helder het beeld wordt gevormd door de verrekijker.
• Houd er rekening mee dat voor een loep met één lens de vergroting negatief is als de objectafstand groter is dan de brandpuntsafstand van de lens. Dit betekent niet dat het gevormde beeld kleiner zal zijn. In dit geval vindt de vergroting nog steeds plaats, maar wordt het gevormde beeld door de waarnemer ondersteboven (top-down) gezien.