- Auteur Jason Gerald [email protected].
- Public 2023-12-16 11:29.
- Laatst gewijzigd 2025-01-23 12:42.
Het optellen van breuken is een zeer nuttige kennis. Deze vaardigheid is heel gemakkelijk te leren en te gebruiken bij het werken aan wiskundige problemen van de basisschool tot de middelbare school. In dit artikel wordt uitgelegd hoe u breuken kunt optellen, zodat u dit in slechts een paar minuten kunt doen.
Stap
Methode 1 van 2: Breuken met dezelfde noemer toevoegen

Stap 1. Controleer de noemer (het getal onder het quotiënt) van elke breuk
Als de getallen hetzelfde zijn, dan tel je breuken met dezelfde noemer op. Als de noemers anders zijn, lees dan de tweede methode.
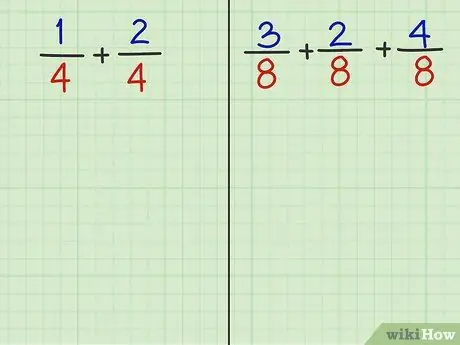
Stap 2. Beantwoord de volgende 2 vragen
Door de laatste stap in deze methode te lezen, zou u de breuken van de volgende twee vragen moeten kunnen optellen.
- Probleem 1: 1/4 + 2/4
- Probleem 2: 3/8 + 2/8 + 4/8
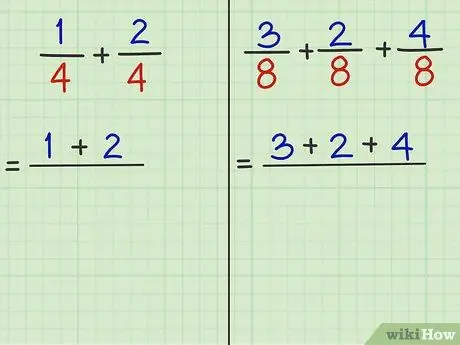
Stap 3. Verzamel de tellers (de getallen boven de deling) en tel ze op
De teller is het getal boven het quotiënt. Het maakt niet uit hoeveel breuken u wilt optellen, u kunt de tellers meteen optellen als de noemers hetzelfde zijn.
- Probleem 1: 1/4 + 2/4 is de op te tellen fractie. "1" en "2" zijn tellers. Dus 1 + 2 = 3.
- Probleem 2: 3/8 + 2/8 + 4/8 is de op te tellen fractie. "3" en "2" en "4" zijn tellers. Dus 3 + 2 + 4 = 9.

Stap 4. Bepaal de nieuwe breuk van de som
Noteer de teller die in stap 2 is verkregen. Dit getal is nieuwe teller. Schrijf de noemer, die hetzelfde getal is onder de bissectrice van elke breuk. U hoeft de berekeningen niet uit te voeren als de noemers hetzelfde zijn. Dit nummer is nieuwe noemer en is altijd gelijk aan de oude noemer als je breuken met dezelfde noemer optelt.
- Probleem 1: 3 is de nieuwe teller en 4 is de nieuwe noemer. Het antwoord op vraag 1 is dus 3/4. 1/4 + 2/4 = 3/4.
- Probleem 2: 9 is de nieuwe teller en 8 is de nieuwe noemer. Het antwoord op vraag 2 is dus 9/8. 3/8 + 2/8 + 4/8 = 9/8.
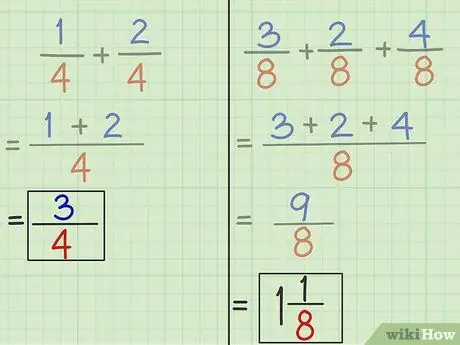
Stap 5. Vereenvoudig breuken indien nodig
Vergeet niet om de nieuwe breuk te vereenvoudigen om het schrijven eenvoudiger te maken.
-
Als de teller groter in plaats van een noemer zoals het resultaat van de optelling van probleem 2, betekent dit dat we 1 hele maand krijgen na het vereenvoudigen van de breuk. Deel de teller door de noemer of 9 gedeeld door 8. Het resultaat is een geheel getal van 1 dat overblijft 1. Schrijf gehele getallen voor de breuk en de rest wordt de teller van een nieuwe breuk met dezelfde noemer.
9/8 = 1 1/8.
Methode 2 van 2: Breuken met verschillende noemers toevoegen

Stap 1. Controleer de noemer (het getal onder het quotiënt) van elke breuk
Als de noemers verschillend zijn, ben je breuken met verschillende noemers optellen. Lees de volgende stappen, want je moet de noemers gelijk maken voordat je breuken toevoegt.
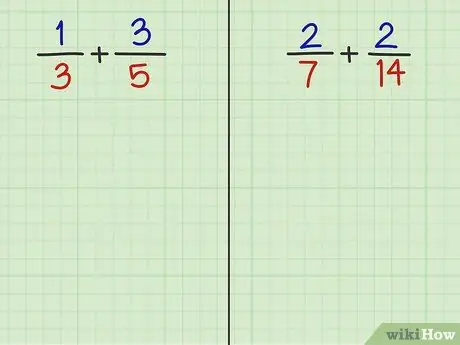
Stap 2. Los de volgende 2 vragen op
Door de laatste stap in deze methode te lezen, zou u de breuken van de volgende twee vragen moeten kunnen optellen.
- Probleem 3: 1/3 + 3/5
- Vraag 4: 2/7 + 2/14

Stap 3. Match de noemers
Om dit te doen, vermenigvuldigt u de noemers van de twee bovenstaande breuken. Een gemakkelijke manier om de noemers gelijk te maken, is door de noemers van de twee breuken te vermenigvuldigen. Als een van de noemers een veelvoud van de andere is, zoek dan het kleinste gemene veelvoud van de twee noemers.
-
Probleem 3:
3 x 5 = 15. De nieuwe noemer van beide breuken is dus 15.
-
Probleem 4:
14 is een veelvoud van 7. Daarom hoeven we alleen 7 met 2 te vermenigvuldigen om 14 te krijgen. De nieuwe noemer van beide breuken is dus 14.

Stap 4. Vermenigvuldig de teller en noemer van de eerste breuk met de noemer van de tweede breuk
Deze stap verandert de waarde van de breuk niet, maar de breuk lijkt te veranderen om overeen te komen met de noemer. De fractionele waarde blijft hetzelfde.
-
Probleem 3:
1/3 x 5/5 = 5/15.
-
Probleem 4:
Voor dit probleem hoeven we alleen de eerste breuk met 2/2 te vermenigvuldigen om de noemers gelijk te krijgen.
2/7 x 2/2 = 4/14

Stap 5. Vermenigvuldig de teller en noemer van de tweede breuk met de noemer van de eerste breuk
Net als bij de bovenstaande stappen veranderen we de waarde van de breuk niet, maar de breuk lijkt te veranderen om de noemer gelijk te maken. De fractionele waarde blijft hetzelfde.
-
Probleem 3:
3/5 x 3/3 = 9/15.
-
Probleem 4:
We hoeven de tweede breuk niet te vermenigvuldigen omdat de noemers hetzelfde zijn.

Stap 6. Schrijf de twee nieuwe breuken op volgorde
Op dit moment hebben we de twee breuken niet bij elkaar opgeteld, hoewel we dat wel kunnen. In de bovenstaande stap hebben we elke breuk met 1 vermenigvuldigd. Nu willen we er zeker van zijn dat de breuken die we willen optellen dezelfde noemer hebben.
-
Probleem 3:
in plaats van 1/3 + 3/5 wordt de breuk 5/15 + 9/15
-
Probleem 4:
In plaats van 2/7 + 2/14 wordt de breuk 4/14 + 2/14

Stap 7. Tel de tellers van de twee breuken bij elkaar op
De teller is het getal boven het quotiënt.
-
Probleem 3:
5 + 9 = 14. 14 is de nieuwe teller.
-
Probleem 4:
4 + 2 = 6. 6 is de nieuwe teller.

Stap 8. Schrijf de gemeenschappelijke noemer (in stap 2) onder de nieuwe teller of gebruik de noemer van de breuk vermenigvuldigd met 1 om de noemer gelijk te maken
-
Probleem 3:
15 is de nieuwe noemer.
-
Probleem 4:
14 is de nieuwe noemer.

Stap 9. Schrijf een nieuwe teller en een nieuwe noemer
-
Probleem 3:
14/15 is het antwoord 1/3 + 3/5 = ?
-
Probleem 4:
6/14 is het antwoord 2/7 + 2/14 = ?

Stap 10. Vereenvoudig en verklein breuken
Om breuken te vereenvoudigen, deelt u de teller en noemer door de grootste gemene deler van de twee getallen.
-
Probleem 3:
14/15 kan niet worden vereenvoudigd.
-
Probleem 4:
6/14 kan worden teruggebracht tot 3/7 na het delen van de teller en de noemer door 2 als de grootste gemene deler van 6 en 14.
Tips
- Voordat u breuken toevoegt, moet u ervoor zorgen dat de noemers hetzelfde zijn.
- Tel de noemers niet op. Als de noemers hetzelfde zijn, gebruik dan het getal als noemer nadat de breuken zijn opgeteld.
- Als je breuken wilt optellen met getallen die bestaan uit hele getallen en breuken, converteer die getallen dan naar breuken en tel ze op volgens de bovenstaande instructies.






