- Auteur Jason Gerald [email protected].
- Public 2024-01-15 08:20.
- Laatst gewijzigd 2025-06-01 06:07.
Het optellen en aftrekken van breuken is een belangrijke vaardigheid om te hebben. Breuken verschijnen de hele tijd in het dagelijks leven, vooral in wiskundelessen, van elementair tot universiteit. Volg deze stappen om te leren hoe u breuken kunt optellen en aftrekken van equivalente breuken, ongelijke breuken, gemengde getallen of gewone breuken. Als je al een manier weet, is het heel eenvoudig om de andere breuken op te lossen!
Stap
Methode 1 van 4: Breuken optellen en aftrekken met dezelfde noemer
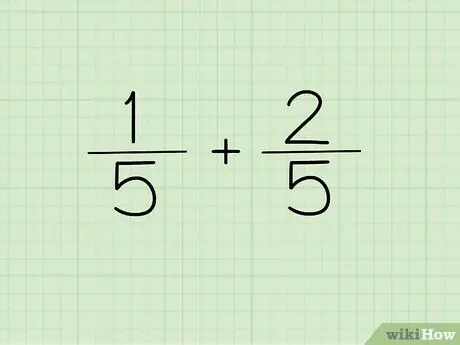
Stap 1. Schrijf je vraag op
Als de noemer van de twee breuken die je wilt optellen of aftrekken hetzelfde is, schrijf dan de noemer één keer op als de noemer van je antwoord.
Met andere woorden, 1/5 en 2/5 hoeven niet te worden geschreven als 1/5 + 2/5 = ?, maar kan worden geschreven als (1+2)/5 = ?. De noemers zijn hetzelfde, dus ze kunnen maar één keer worden geschreven. De twee tellers worden gecombineerd
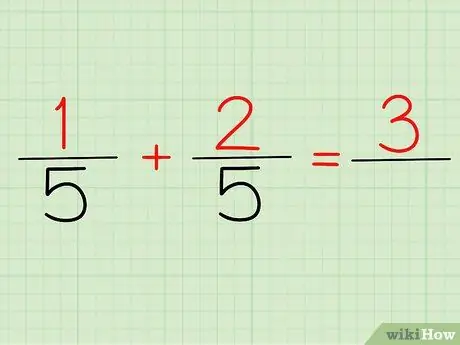
Stap 2. Tel de tellers op
De teller is het getal dat boven een breuk staat. Als we naar het bovenstaande probleem kijken, zijn 1/5 en 2/5, 1 en 2 onze tellers.
Of je het nu 1/5 + 2/5 of (1+2)/5 schrijft, je antwoord is hetzelfde: 3! Omdat, 1 + 2 = 3

Stap 3. Laat de noemer staan
Aangezien de noemers hetzelfde zijn, doe niets met de noemers! Niet optellen, aftrekken, vermenigvuldigen of delen. Laat maar zo.
Dus uit hetzelfde voorbeeld is onze noemer 5. Juist! 5 is het onderste getal van onze breuk. We hebben de helft van het antwoord

Stap 4. Schrijf je antwoord op
Nu hoef je alleen nog maar je teller en noemer op te schrijven! Als u het bovenstaande voorbeeld gebruikt, is uw antwoord 3/5.
Wat is jouw teller? 3. Uw noemer? 5. Daarom is 1/5 + 2/5 of (1+2)/5 gelijk aan 3/5.
Methode 2 van 4: Breuken optellen en aftrekken met verschillende noemers

Stap 1. Zoek de kleinste gemene deler
Dat wil zeggen, de kleinste noemer is hetzelfde voor beide breuken. Stel dat we de breuken 2/3 en 3/4 hebben. Wat is de noemer? 3 en 4. Om de kleinste gemene deler van beide breuken te vinden, kun je dit op drie manieren doen:
- Schrijf de veelvouden van. Veelvouden van 3 zijn 3, 6, 9, 12, 15, 18 … enzovoort. Veelvouden van 4? 4, 8, 12, 16, 20, enzovoort. Wat is het kleinste getal dat een veelvoud is van de twee? 12! Dat is de kleinste gemene deler.
-
Ontbinding in priemfactoren. Als je van factoren weet, kun je priemfactorisatie uitvoeren. Dat wil zeggen, u zoekt naar de getallen waaruit uw noemer bestaat. Voor nummer 3 zijn de factoren 3 en 1. Voor nummer 4 zijn de factoren 2 en 2. Dan jullie allemaal. 3 x 2 x 2 = 12. Je kleinste gemene deler!
Vermenigvuldig alle getallen voor het kleinere getal. In sommige opgaven, zoals deze, kun je beide getallen vermenigvuldigen - 3 x 4 = 12. Als je echter een grote noemer hebt, doe dit dan niet! Je wilt niet 56 x 44 vermenigvuldigen en er alles aan doen om 2.464 te krijgen

Stap 2. Vermenigvuldig de noemer met het getal dat nodig is om de kleinste gemene deler te krijgen
Met andere woorden, u wilt dat al uw noemers gelijk zijn. In ons voorbeeld willen we dat de noemer 12 is. Om 3 in 12 te veranderen, vermenigvuldigt u 3 met 4. Om 4 te veranderen in 12, vermenigvuldigt u 4 met 3. Dezelfde noemer zal de noemer zijn van uw uiteindelijke antwoord.
-
Dus 2/3 wordt 2/3 x 4 en 3/4 wordt 3/4 x 3. Dat wil zeggen, we hebben nu 2/12 en 3/12. Maar, we zijn nog niet klaar!
- Je zult zien dat de noemers met elkaar worden vermenigvuldigd. Dit kan in deze situatie, maar niet in alle situaties. Soms kunt u, in plaats van beide noemers te vermenigvuldigen, beide noemers met een ander getal vermenigvuldigen om het kleinere getal te krijgen.
- In andere opgaven moet je soms één noemer vermenigvuldigen om hem gelijk te maken aan de noemer van de andere breuk in de opgave.

Stap 3. Vermenigvuldig de teller met hetzelfde getal
Als je de noemer met een getal vermenigvuldigt, moet je ook de teller met hetzelfde getal vermenigvuldigen. Wat we in de laatste stap hebben gedaan, is slechts een deel van de vermenigvuldiging die moet worden gedaan.
We hebben 2/3x4 en 2/4x3 als de eerste stap - dan, in de tweede stap, 2 x 4/3 x 4 en 3 x 3/4 x 3. Dat wil zeggen, onze nieuwe nummers zijn 8/12 en 9/ 12. Perfect
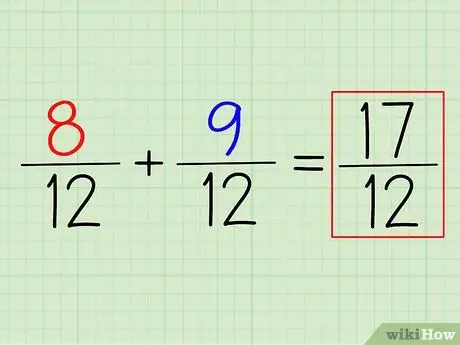
Stap 4. Tel de tellers op (of trek ze af) om het antwoord te krijgen
Om 8/12 + 9/12 op te tellen, hoef je alleen maar de tellers op te tellen. Onthoud: laat de noemer gewoon staan. De kleinste gemene deler die je vindt, is je uiteindelijke noemer.
In dit voorbeeld (8+9)/12 = 17/12. Om het naar een gemengd getal om te zetten, trekt u gewoon de noemer van de teller af en schrijft u de rest op. In dit geval 17/12 = 1 5/12
Methode 3 van 4: Gemengde en gewone breuken optellen en aftrekken
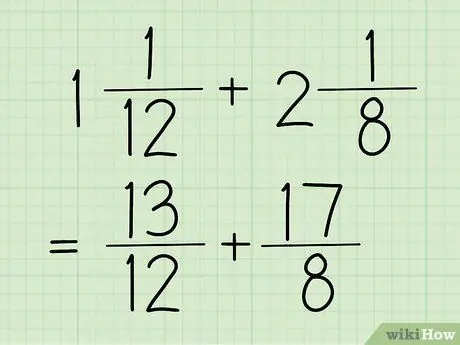
Stap 1. Converteer uw gemengde breuken naar gewone breuken
Een gemengd getal is een breuk met een geheel getal en een breuk, zoals in het bovenstaande voorbeeld (1 5/12). Ondertussen is een gewone breuk een breuk waarvan de teller (bovenste getal) groter is dan de noemer (onderste getal). Deze fractie wordt ook gezien in de vorige stap, die 17/12 is.
Voor de voorbeelden in deze sectie gebruiken we 13/12 en 17/8

Stap 2. Zoek een gemene deler
Herinner je je de drie manieren om de kleinste gemene deler te vinden? Door veelvouden te schrijven, priemfactorisatie te gebruiken of de noemers te vermenigvuldigen.
Laten we veelvouden van ons voorbeeld 12 en 8 zoeken. Wat is het kleinste getal dat beide gemeen hebben? 24. 8, 16, 24 en 12, 24 - bingo

Stap 3. Vermenigvuldig je teller en noemer om de equivalente breuk te vinden
Beide noemers moeten veranderd worden in 24. Hoe zet je 12 om in 24? Vermenigvuldigen met 2. 8 tot 24? Vermenigvuldigen met drie. Maar vergeet niet - je moet de tellers ook vermenigvuldigen!
Dus (13 x 2)/(12 x 2) = 26/24. En (17 x 3)/(8 x 3) = 51/24. We zijn er bijna klaar mee

Stap 4. Tel je breuken op of trek ze af
Nu je dezelfde noemer hebt, kun je de twee tellers eenvoudig bij elkaar optellen. Onthoud, laat de noemer gewoon staan!
26/24 + 51/24 = 77/24. Dat is jouw som! De cijfers bovenaan waren echter te groot…

Stap 5. Zet je antwoord terug naar gemengde getallen
Het zeer grote getal bovenaan de breuk voelt een beetje vreemd aan - je kunt de grootte van je breuk niet zien. Het enige dat u hoeft te doen, is uw noemer herhaaldelijk van de teller aftrekken totdat deze niet verder kan worden afgetrokken en de rest opschrijven.
-
In dit voorbeeld 77 min 24 bij 3 keer. Dat wil zeggen, 24 x 3 = 72. De rest is 5! Dus wat is je eindresultaat? 3 5/24.
Helemaal waar!
Methode 4 van 4: Breuken optellen en aftrekken zonder LCM te vinden
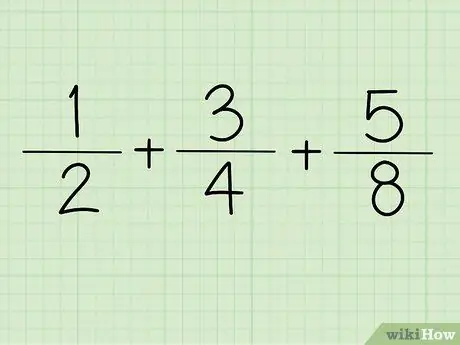
Stap 1. Schrijf de breuk op
Bijvoorbeeld + +

Stap 2. Los eerst de teller op
- Vermenigvuldig met de teller van de andere breuk.
- Vermenigvuldig 1 met 4 en 8. [32]
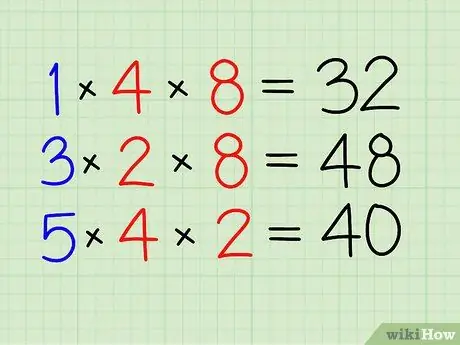
Stap 3. Doe hetzelfde voor de andere breuken
- Vermenigvuldig 3 met 2 en 8. [48]
- Vermenigvuldig tot slot 5 met 4 en 2. [40]
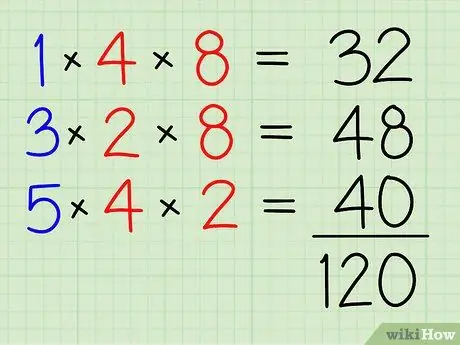
Stap 4. Voeg ze allemaal samen
32+48+40=120
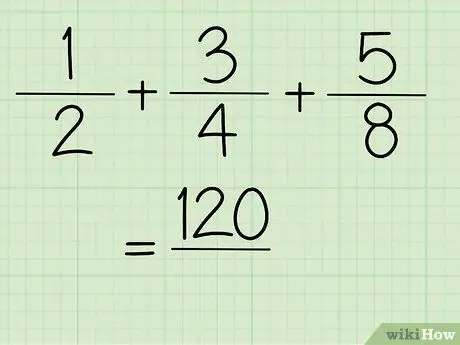
Stap 5. Nu krijgt u de tellerwaarde

Stap 6. Los de noemer van de breuk op

Stap 7. Vermenigvuldig de noemers van alle breuken
2×4×8=64

Stap 8. Nu krijg je het resultaat
120/64 = 1 56/64 = 1 ⅞
Waarschuwing
- Met deze methode kunt u grote getallen vermenigvuldigen.
- Mogelijk hebt u een rekenmachine nodig om op deze manier te berekenen.






