IQR is het interkwartielbereik of het kwartielwortelbereik van een dataset. IQR wordt gebruikt in statistische analyse om conclusies te trekken over een dataset. IQR wordt vaker gebruikt dan bereik omdat IQR niet de buitenste gegevens bevat. Lees verder om te leren hoe u de IQR kunt vinden!
Stap
Methode 1 van 3: IQR begrijpen
Stap 1. Begrijp hoe u IQR kunt gebruiken
Kortom, IQR is een manier om de verspreiding van een reeks getallen te begrijpen. Het bereik van het wortelkwartiel wordt gedefinieerd als het verschil tussen het bovenste kwartiel (25% boven) en het onderste kwartiel (25% laagste) van de dataset.
Tip:
Het onderste kwartiel wordt meestal geschreven als Q1 en het bovenste kwartiel wordt geschreven als Q3 - waardoor het middelpunt van de gegevens technisch gezien Q2 is en het hoogste punt Q4.
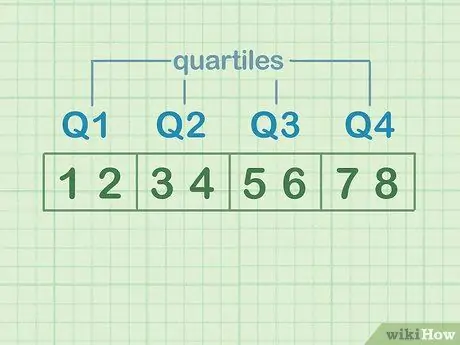
Stap 2. Begrijp de kwartielen
Om kwartielen te illustreren, verdeelt u de reeks getallen in vier gelijke delen. Elk van deze delen is een "kwartiel". Stel dat de datasets zijn: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 en 2 zijn het eerste kwartiel of Q1
- 3 en 4 zijn het tweede kwartiel of Q2
- 5 en 6 zijn het derde kwartiel of Q3
- 7 en 8 zijn het vierde kwartiel of Q4
Stap 3. Leer de formule
Om het verschil tussen het bovenste en onderste kwartiel te vinden, moet u het 75e percentiel van het 25e percentiel aftrekken.
De formule is geschreven: Q3 – Q1 = IQR
Methode 2 van 3: De gegevensset samenstellen
Stap 1. Verzamel uw gegevens
Als je IQR in de klas en in tests bestudeert, krijg je mogelijk een set gegevens die al zijn voorbereid, bijvoorbeeld 1, 4, 5, 7, 10. Dit is je dataset - de cijfers waarmee je gaat werken. U kunt echter uw eigen cijfers samenstellen uit tabelvragen of verhaalproblemen.
Zorg ervoor dat elk nummer hetzelfde voorstelt:
bijvoorbeeld het aantal eieren in elk nest van een bepaalde vogelpopulatie, of het aantal parkeerplaatsen in elk huis in een bepaald blok.
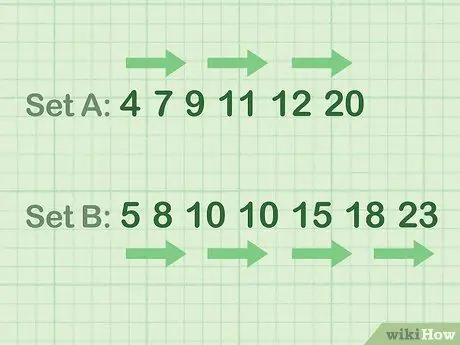
Stap 2. Sorteer uw gegevens in oplopende volgorde
Met andere woorden: rangschik de getallen van klein naar groot. Gebruik de tips uit de volgende voorbeelden.
- Voorbeeld van even getalgegevens (Set A): 4 7 9 11 12 20
- Voorbeeld van oneven nummergegevens (Set B): 5 8 10 10 15 18 23
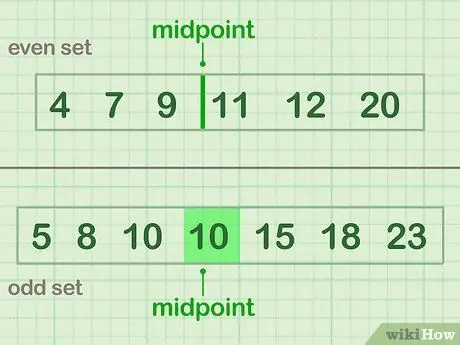
Stap 3. Verdeel de gegevens in tweeën
Om in tweeën te splitsen, zoekt u het middelpunt van uw gegevens: het aantal of de getallen die zich in het midden van de gegevensset bevinden. Als je een oneven aantal gegevens hebt, kies dan het getal dat precies in het midden staat. Als je een even aantal gegevens hebt, ligt het middelpunt tussen de twee middelste getallen.
- Een even voorbeeld (Set A) met een middelpunt tussen 9 en 11: 4 7 9 | 11 12 20
- Een vreemd voorbeeld (set B) met een middelpunt van waarde (10): 5 8 10 (10) 15 18 23
Methode 3 van 3: IQR berekenen
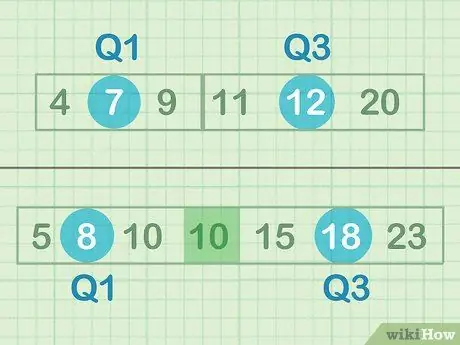
Stap 1. Zoek de mediaan van uw onderste en bovenste helft van de gegevens
De mediaan is het "middelpunt" of het getal dat zich in het midden van een reeks getallen bevindt. In dit geval zoekt u niet naar het middelpunt van alle getallen, maar zoekt u naar het relatieve middelpunt van de bovenste en onderste gegevenssubsets. Als u een oneven aantal gegevens heeft, hoeft u het middelste getal niet op te nemen - in set B hoeft u bijvoorbeeld geen enkele 10 op te nemen.
-
Zelfs voorbeeld (set A):
- Mediaan van de onderste helft van de gegevens = 7 (Q1)
- Mediaan van de bovenste helft van de gegevens = 12 (Q3)
-
Vreemd voorbeeld (set B):
- Mediaan van de onderste helft van de gegevens = 8 (Q1)
- Mediaan van de bovenste helft van de gegevens = 18 (Q3)
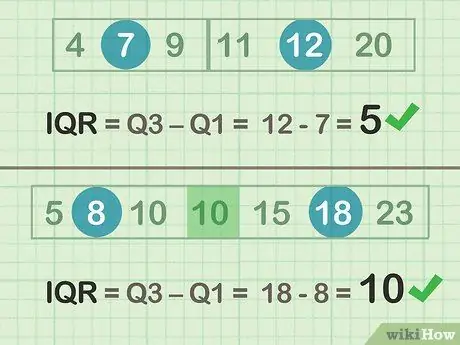
Stap 2. Trek Q3-Q1 af om de IQR te bepalen
Nu weet je hoeveel getallen tussen het 25e en 75e percentiel vallen. U kunt dit nummer gebruiken om de verspreiding van gegevens te begrijpen. Als een test bijvoorbeeld een maximale score van 100 heeft en de IQR van de score 5 is, kun je ervan uitgaan dat de meeste mensen die de test doen bijna hetzelfde begrip hebben, omdat het bereik van hoogte- en dieptepunten niet erg groot is. Als de IQR van een testscore 30 is, begin je je misschien af te vragen waarom sommige mensen zo hoog scoren en anderen zo laag.
- Zelfs voorbeeld (set A): 12 -7 = 5
- Vreemd voorbeeld (set B): 18 – 8 = 10
Tips
Het is belangrijk om dit zelf te leren doen. Er zijn echter verschillende online IQR-calculators die u kunt gebruiken om uw werk te controleren. Vertrouw niet te veel op rekenmachine-apps als je dit in de klas leert! Als u wordt gevraagd om de IQR in een test op te zoeken, moet u weten hoe u deze handmatig kunt vinden
Gerelateerde WikiHoe
- Uitbijters detecteren
- Hoe het bereik van een gegevensset te berekenen?
- Hoe maak je een doos- en tentdiagram
