- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Laatst gewijzigd 2025-06-01 06:07.
Aftrekken is simpelweg het ene getal van het andere aftrekken. Het is gemakkelijk om het ene geheel getal van het andere af te trekken, maar aftrekken kan lastig zijn als je breuken of decimalen aftrekt. Zodra u aftrekken begrijpt, kunt u complexere wiskundige concepten gebruiken en kunt u gemakkelijker getallen optellen, vermenigvuldigen en delen.
Stap
Methode 1 van 6: Grote gehele getallen aftrekken door te lenen

Stap 1. Schrijf een groot aantal op
U wilt bijvoorbeeld 32 - 17 oplossen. Schrijf eerst 32 op.

Stap 2. Schrijf het kleinere getal er direct onder
Zorg ervoor dat je de tientallen en enen waarden in de juiste kolommen plaatst, zodat 3 van 32 direct boven 1 van 17 staat en 2 van 32 direct boven 7 van 17.
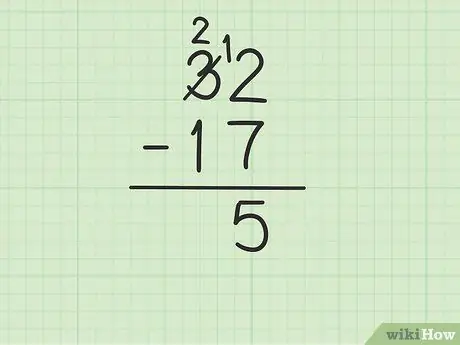
Stap 3. Trek het bovenste getal in de kolom eenheden af van het getal onderaan
Dit kan echter ingewikkeld worden als het onderste getal groter is dan het bovenste getal. In dit geval is 7 groter dan 2. Dit is wat u moet doen:
- Je moet lenen van het getal 3 van 32 (ook wel groeperen genoemd), om 2 in 12 te veranderen.
- Kruis het cijfer 3 van de 32 aan en vervang het door het cijfer 2, terwijl het cijfer 2 12 wordt.
- Nu kun je 12 - 7 aftrekken, wat gelijk is aan 5. Schrijf 5 onder de twee getallen die je aftrekt, zodat ze in de eenhedenkolom van de nieuwe rij staan.
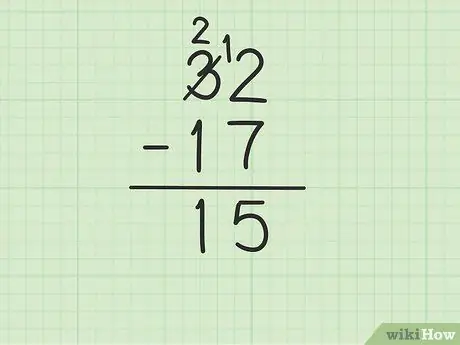
Stap 4. Trek het bovenste getal in de tientallenkolom af van het onderste getal
Onthoud dat 3 2 is geworden. Trek nu 1 af van 17 van 2 hierboven om (2-1) te krijgen. Schrijf 1 hieronder, in de tientallenkolom, links van 5 in de eenhedenkolom. Je schrijft 15. Dat wil zeggen, 32 - 17 = 15.
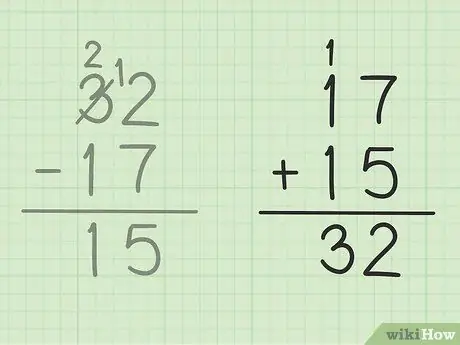
Stap 5. Controleer je werk
Als je er zeker van wilt zijn dat je twee getallen correct hebt afgetrokken, hoef je alleen maar je antwoord op te tellen bij het kleinere getal om een groot getal te krijgen. In dit probleem moet je je antwoord, 15, optellen bij het kleinere aantal aftrekkingen, 17. 15 + 17 = 32, zodat je antwoord correct is. Veilig!
Methode 2 van 6: Kleine gehele getallen aftrekken
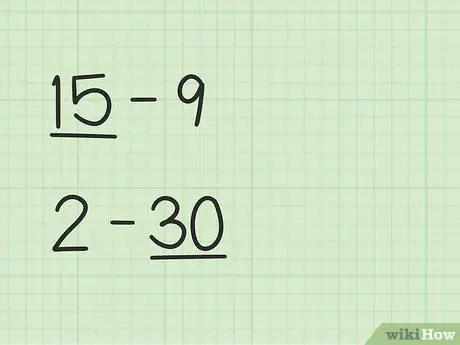
Stap 1. Zoek het grotere getal
Problemen zoals 15 -9 zullen een andere manier hebben dan 2 - 30.
- Bij de vragen 15 t/m 9 is het eerste getal, 15, groter dan het tweede getal, 9.
- Bij vragen 2 t/m 30 is het tweede getal, 30, groter dan het eerste getal, 2.
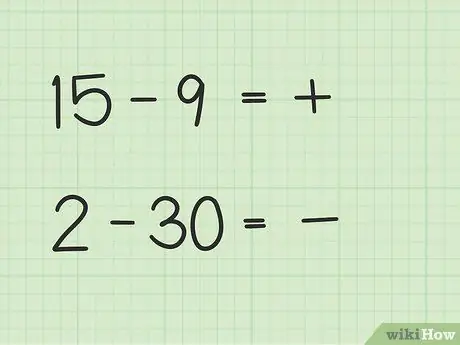
Stap 2. Bepaal of je antwoord positief of negatief zal zijn
Als het eerste getal groter is, is het antwoord positief. Als het tweede getal groter is, is het antwoord negatief.
- In de eerste vraag, 15 - 9, is uw antwoord positief omdat het eerste getal groter is dan het tweede getal.
- In de tweede vraag, 2 - 30, is uw antwoord negatief omdat het tweede getal groter is dan het eerste getal.
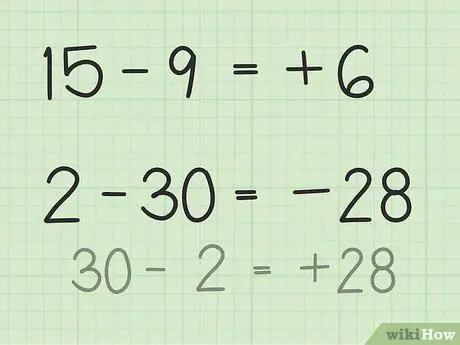
Stap 3. Zoek het verschil tussen twee getallen
Om twee getallen af te trekken, moet je je het verschil tussen de twee getallen voorstellen en de getallen ertussen berekenen.
- Stel je voor vragen 15 - 9 een stapel van 15 pokerchips voor. Gooi 9 fiches weg en slechts 6. Dus 15 - 9 = 6. Je kunt je ook een getallenlijn voorstellen. Denk aan de getallen van 1 tot 15, gooi dan 9 eenheden weg of geef ze terug zodat je 6 krijgt.
- Voor vragen 2 - 30 is de eenvoudigste manier om dit op te lossen door het getal om te keren en het resultaat negatief te maken na aftrekken. Dus 30 - 2 = 28 dus 28 en 30 hebben een verschil van 2. Maak nu het resultaat negatief omdat je al hebt vastgesteld dat het antwoord negatief is omdat het tweede getal groter is dan het eerste getal. Dus 2 - 30 = -28.
Methode 3 van 6: Decimalen aftrekken
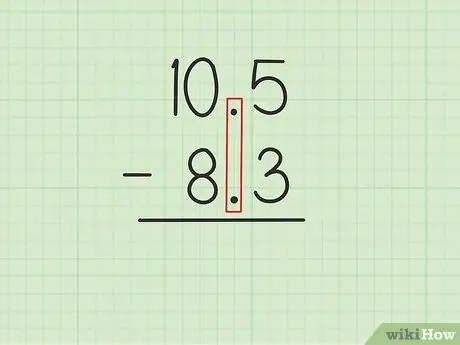
Stap 1. Schrijf het grotere getal over het kleinere getal met de decimale punten uitgelijnd
Stel dat je de volgende problemen wilt oplossen: 10, 5 - 8, 3. Schrijf 10, 5 over 8, 3 zodat de decimale punten van de twee getallen evenwijdig zijn., 5 van 10, 5 moet direct boven zijn, 3 van 8, 3 en 0 van 10, 5 moet boven 8 van 8, 3 zijn.
Als je een probleem hebt omdat de twee getallen niet hetzelfde getal achter de komma hebben, schrijf dan 0 in de blanco totdat de som van de getallen hetzelfde is. Het probleem is bijvoorbeeld 5, 32 - 4, 2, u kunt het schrijven als 5, 32 - 4, 2 0. Dit verandert de waarde van het tweede getal niet, maar maakt het aftrekken van de twee getallen gemakkelijker.

Stap 2. Trek het bovenste getal in de tientallenkolom af van het onderstaande getal
In dit geval moet je 3 van 5 aftrekken. 5 - 3 = 2, dus je moet 2 onder 3 van 8, 3 schrijven.
Zorg ervoor dat je een decimaalteken in het antwoord zet, zodat er staat, 2

Stap 3. Trek het getal boven de kolom eenheden af van het getal eronder
Je moet 8 van 0 aftrekken. Leen 1 van het tientallengedeelte om 0 te veranderen in 10 en trek 10 - 8 af om 2 te krijgen. Je kunt ook 10 - 8 tellen zonder te lenen omdat er geen getallen in de tweede tientallenkolom staan. Schrijf het antwoord onder 8, links van de komma.

Stap 4. Schrijf je eindresultaat op
Uw eindresultaat is 2, 2.

Stap 5. Controleer je werk
Als je er zeker van wilt zijn dat je decimale aftrekking correct is, hoef je alleen maar je antwoord op te tellen met het kleinere getal om het grotere getal te krijgen. 2, 2 + 8, 3 = 10, 5, dus je bent klaar.
Methode 4 van 6: breuken aftrekken

Stap 1. Lijn de noemer en teller van de breuk uit
Stel dat u problemen 13/10 - 3/5 wilt oplossen. Schrijf het probleem zo op dat de twee tellers, 13 en 3 en de twee noemers, 10 en 5 tegenover elkaar staan. Deze twee getallen worden gescheiden door een aftrekteken. Dit zal u helpen het probleem te visualiseren en het gemakkelijker op te lossen.

Stap 2. Zoek de kleinste gemene deler
De kleinste gemene deler is het kleinste getal dat door twee getallen kan worden gedeeld. In dit voorbeeld moet je de kleinste gemene deler vinden die deelbaar is door 10 en 5. Je zult zien dat 10 de kleinste gemene deler is voor beide getallen omdat 10 deelbaar is door 10 en 5.
Merk op dat de kleinste gemene deler van twee getallen er niet altijd één van is. De kleinste gemene deler voor 3 en 2 is bijvoorbeeld 6 omdat 6 het kleinste getal is dat door twee getallen kan worden gedeeld
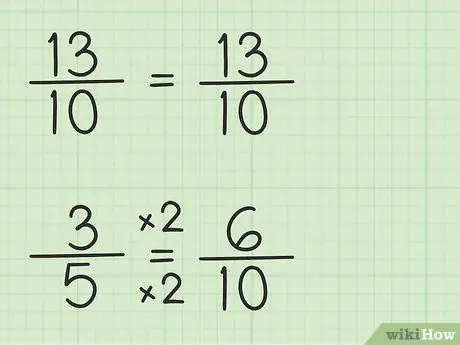
Stap 3. Schrijf de breuken op met dezelfde noemer
De breuk 13/10 kan op dezelfde manier worden geschreven omdat de noemer 10 is, de kleinste gemene deler, dat is 10 maal 1. De breuk 3/5 moet echter worden herschreven omdat de noemer 5 is, de kleinste gemene deler, wat 10 is, maal 2. Dus de breuk 3/5 moet worden vermenigvuldigd met 2/2 om de noemer 10 te maken, dus 3/5 x 2/2 = 6/10. Je hebt de equivalente breuk gevonden. 3/5 is gelijk aan 6/10, hoewel u met 6/10 het eerste getal, 13/10, kunt aftrekken.
Schrijf een nieuwe vraag als volgt: 13/10 - 6/10
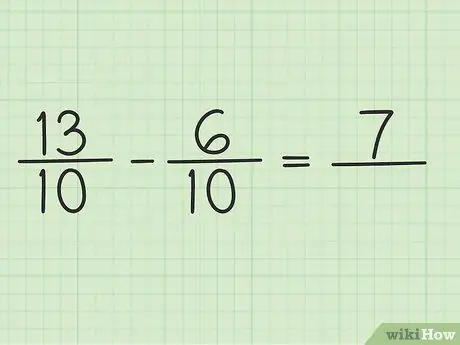
Stap 4. Trek de teller af tot twee getallen
Trek gewoon 13 - 6 af, zodat het resultaat 7 is. Je kunt de noemer van de breuk niet veranderen.
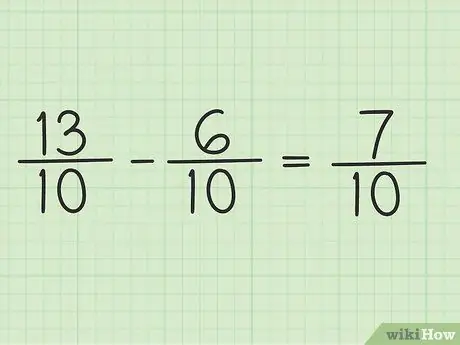
Stap 5. Schrijf de nieuwe teller over dezelfde noemer om het eindresultaat te krijgen
De nieuwe teller is 7. Beide breuken hebben een noemer van 10. Je eindresultaat is 7/10.
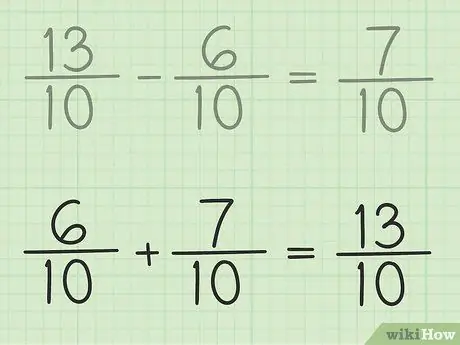
Stap 6. Controleer je werk
Als je zeker wilt weten dat je de breuk correct aftrekt, tel dan je antwoord en de kleinere breuk bij elkaar op, zodat het resultaat een grotere breuk is. 7/10 + 6/10 = 13/10. Het is klaar.
Methode 5 van 6: Breuken aftrekken van hele getallen

Stap 1. Schrijf het probleem op
Stel dat u het volgende probleem wilt oplossen: 5 -. Schrijf het op.
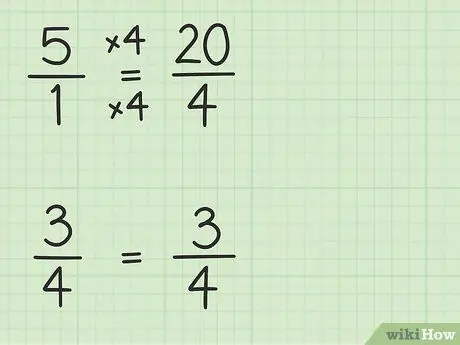
Stap 2. Zet gehele getallen om in breuken die dezelfde noemer hebben als andere breuken
Je converteert 5 naar een breuk met een noemer van 4 om twee getallen te kunnen aftrekken. Dus je moet 5 zien als een breuk van 5/1. Vervolgens kunt u de teller en noemer van de nieuwe breuk vermenigvuldigen met 4 om de noemers van de twee getallen hetzelfde te maken. Dus 5/1 x 4/4 = 20/4. Deze breuk is gelijk aan 5, maar je kunt er twee getallen van aftrekken.
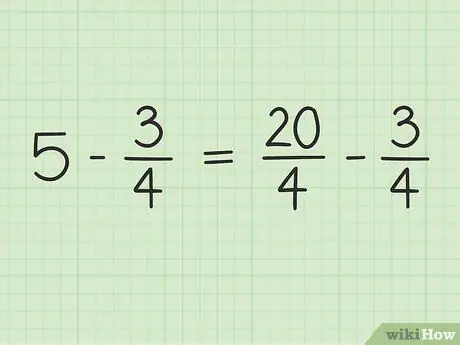
Stap 3. Herschrijf het probleem
De nieuwe opgave kan als volgt worden geschreven: 20/4 - 3/4.
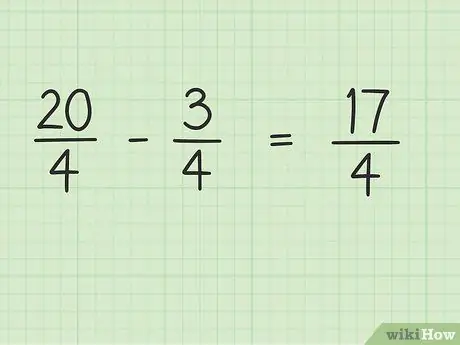
Stap 4. Trek de teller van de breuk af, terwijl de noemer hetzelfde blijft
Trek nu gewoon 20 bij 3 af om het eindresultaat te krijgen. 20 - 3 = 17, dus 17 is de nieuwe teller. Je kunt de noemer hetzelfde laten.
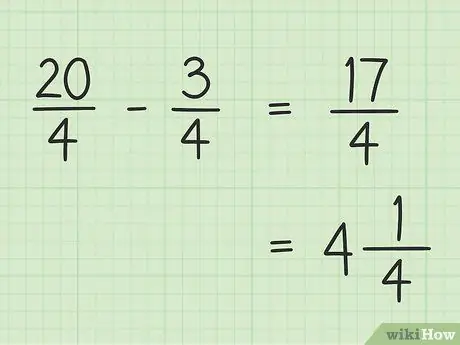
Stap 5. Schrijf je eindresultaat op
Je eindresultaat is 17/4. Als je het als een gemengd getal wilt schrijven, deel je 17 door 4 zodat het resultaat 4 is en de rest 1 is, zodat je uiteindelijke 17/4 gelijk is aan 4.
Methode 6 van 6: Variabelen aftrekken
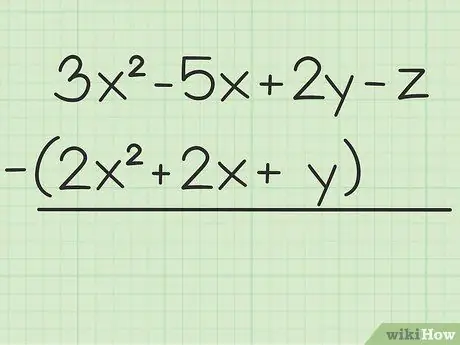
Stap 1. Schrijf het probleem op dat je wilt oplossen
Bijvoorbeeld de volgende vraag: 3x2 - 5x + 2j - z - (2x2 + 2x + j). Schrijf de eerste set variabelen over de tweede.
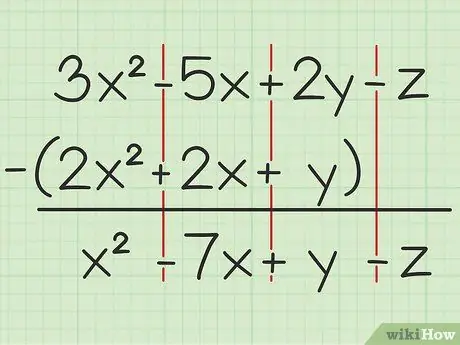
Stap 2. Trek dezelfde variabelen af
Als je een variabele tegenkomt, kun je alleen dezelfde variabele optellen of aftrekken die met dezelfde kwadraatgraad is geschreven. Dat betekent dat je 4x. kunt aftrekken2 vanaf 7x2, maar kan 4x niet aftrekken van 4y. U kunt het probleem dus als volgt opsplitsen:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2j - y = y
- -z - 0 = -z
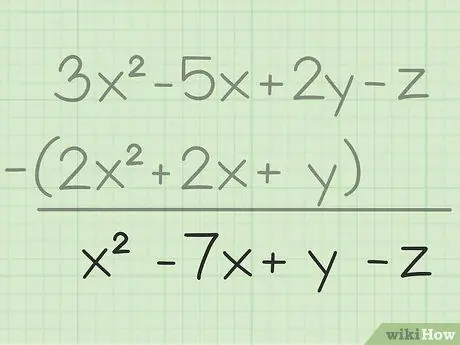
Stap 3. Schrijf je eindresultaat op
Je hebt alle variabelen afgetrokken, het enige wat je hoeft te doen is je uiteindelijke resultaat te schrijven dat alle variabelen bevat die je hebt afgetrokken. Hier is het eindresultaat:






