- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Laatst gewijzigd 2025-01-23 12:42.
Leerlingen die nog erg jong zijn, hebben vaak moeite om het begrip aftrekken te begrijpen. Als je een leraar bent en het concept van aftrekken aan studenten wilt onderwijzen, probeer het concept dan op een manier weer te geven die interessant en begrijpelijker is voor studenten. Nadat je de basisconcepten van aftrekken hebt uitgelegd, probeer je verder te gaan met het concept van tweecijferig aftrekken. Als leerlingen het eenmaal goed onder de knie hebben, probeer dan verschillende concepten uit te leggen die ze kunnen gebruiken om aftrekproblemen op te lossen, zoals Common Core.
Stap
Methode 1 van 4: Aftrekken leren via objecten of afbeeldingen

Stap 1. Schrijf of presenteer een verhaalprobleem met een aftrekprobleem aan de leerlingen:
Er staan 8 sinaasappels op tafel, 3 sinaasappels worden door Jordan gegeten. Hoeveel sinaasappels zijn er nog?
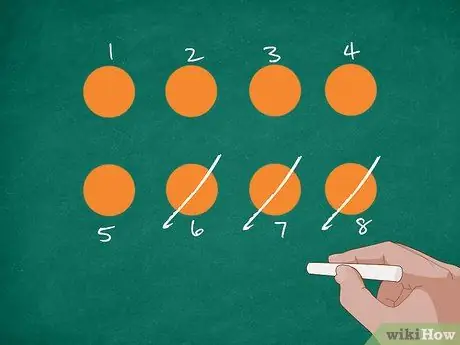
Stap 2. Vertegenwoordig het probleem met afbeeldingen
Teken eerst 8 oranje cirkels op het bord of een stuk papier. Laat de leerlingen daarna het nummer tellen en label elke cirkel met een nummer. Doorstreep 3 cirkels terwijl je uitlegt dat Jordan 3 sinaasappels heeft gegeten. Vraag de leerlingen hoeveel sinaasappels er nu nog over zijn.
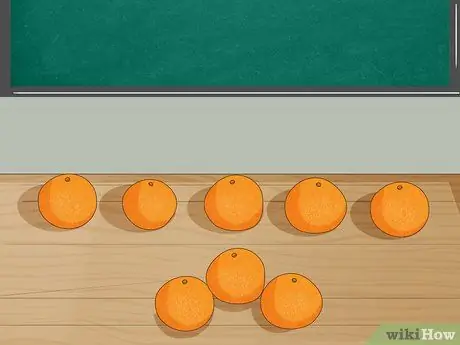
Stap 3. Vertegenwoordig het probleem met objecten
Leg 8 sinaasappels op tafel en vraag de leerlingen het aantal te tellen. Neem daarna 3 sinaasappels van de tafel en leg uit dat Jordan 3 sinaasappels heeft gegeten. Laat de leerlingen het aantal overgebleven sinaasappels tellen.

Stap 4. Schrijf de vergelijking op
Leg uit dat verhaalproblemen ook kunnen worden weergegeven door middel van een vergelijking. Zorg ervoor dat je ze altijd begeleidt bij het omzetten van verhaalproblemen in wiskundige vergelijkingen.
- Vraag hoeveel sinaasappels er op tafel staan. Schrijf het cijfer "8" op het bord.
- Vraag hoeveel sinaasappels Jordan heeft gegeten. Schrijf het cijfer "3" op het bord.
- Vraag de leerlingen of dit een optel- of aftrekprobleem is. Schrijf een "-" teken tussen de cijfers "8" en "3".
- Laat de leerlingen antwoorden zoeken op de vergelijking "8-3". Schrijf een "=" teken gevolgd door het cijfer "5".
Methode 2 van 4: Aftrekken leren met de aftelmethode op de getallenlijn

Stap 1. Schrijf of presenteer een verhaalprobleem met een aftrekprobleem aan de leerlingen:
Er zijn 10 honden in de dierenwinkel, waarvan er 6 zijn geadopteerd door hun nieuwe eigenaren. Hoeveel honden zijn er nog in de dierenwinkel?
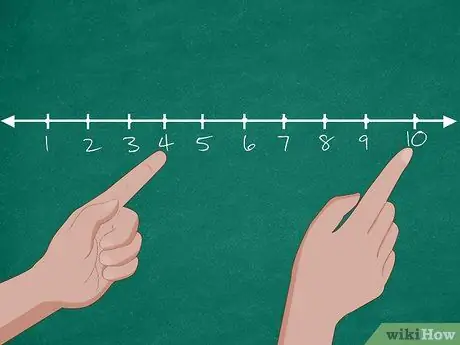
Stap 2. Gebruik de hulp van een getallenlijn om het probleem op te lossen
Teken eerst een getallenlijn met de getallen 0-10 op het bord. Vraag de leerlingen daarna om het aantal honden in de dierenwinkel te noemen. Nadat de leerlingen hebben geantwoord, omcirkelt u het cijfer '10' op het bord. Vraag dan nogmaals hoeveel honden er zijn geadopteerd. Als de leerlingen "6" antwoorden, vraag ze dan om 6 nummers af te tellen vanaf 10 (9, 8, 7, 6, 5, 4) totdat ze het nummer "4" hebben bereikt. Vraag daarna opnieuw hoeveel honden er nog in de dierenwinkel zijn.

Stap 3. Schrijf de vergelijking op
Leg uit dat verhaalproblemen ook kunnen worden weergegeven door middel van een vergelijking. Zorg ervoor dat je ze altijd begeleidt bij het omzetten van verhaalproblemen in wiskundige vergelijkingen.
- Vraag hoeveel honden er in de dierenwinkel zijn. Schrijf het cijfer "10" op het bord.
- Vraag hoeveel honden zijn geadopteerd. Schrijf het cijfer "6" op het bord.
- Vraag de leerlingen of dit een optel- of aftrekprobleem is. Schrijf een "-" teken tussen de cijfers "10" en "6".
- Laat de leerlingen antwoorden zoeken op de vergelijking "10-6". Schrijf een "=" teken gevolgd door het cijfer "4".
Methode 3 van 4: Aftrekken leren door middel van feitenfamilieconcepten

Stap 1. Introduceer het concept van feitenfamilie aan studenten
In feite is een feitenfamilie een groep wiskundige problemen die uit dezelfde getallen bestaat. De getallen 10, 3 en 7 vormen bijvoorbeeld een feitenfamilie. De drie getallen kunnen op verschillende manieren worden opgeteld of afgetrokken; U kunt twee vergelijkingen genereren met alleen deze 3 getallen:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Stap 2. Schrijf of presenteer een verhaalprobleem met een aftrekprobleem aan de leerlingen:
Ik heb 7 snoepjes. Als ik 3 snoepjes eet, hoeveel snoepjes blijven er dan over?

Stap 3. Gebruik het feitfamilieconcept om het probleem op te lossen
Begeleid de leerlingen stap voor stap door het proces:
- Vraag de leerlingen welk probleem ze willen oplossen. Schrijf "7-3=?" op het krijtbord.
- Vraag hen om het derde lid van de fact-familiegroep te identificeren. Schrijf de volgende vergelijkingen op het bord: “3+_=7”; “_+3=7”; "; “7-_=3”; en 7-3=_” Vraag de cursisten daarna om de resultaten te lezen en het probleem in te vullen met de antwoorden die ze hebben gegeven.
Methode 4 van 4: Introductie van gemeenschappelijke kernconcepten
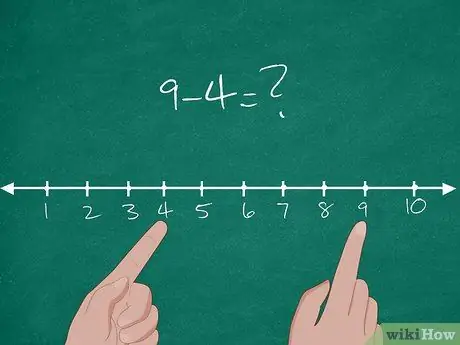
Stap 1. Leer het concept van aftrekken in Common Core
In feite is Common Core een nieuwe leerstandaard die door de meeste staten in Amerika wordt toegepast. In Common Core wordt het basisconcept van aftrekken verklaard door de afstand tussen twee getallen. Om het concept aan de leerlingen uit te leggen, tekent u een getallenlijn met de getallen 1-10 op het bord.
- Geef daarna een basisaftrekprobleem aan de leerlingen: 9-4=?.
- Zoek de locatie van het cijfer 4 op de getallenlijn. Leg de leerlingen uit dat deze locatie hun vertrekpunt is.
- Zoek de locatie van het cijfer 9 op de getallenlijn. Leg aan de leerlingen uit dat de locatie de eindbestemming is.
- Vraag de leerlingen daarna om de afstand tussen de twee getallen te meten of te berekenen: "5, 6, 7, 8, 9".
- De afstand tussen de twee getallen is 5. Dus 9-4=5.
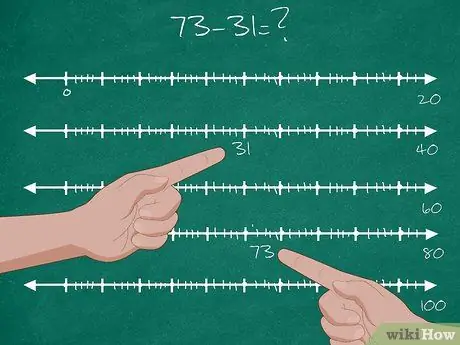
Stap 2. Laat de leerlingen het tweecijferige aftrekprobleem oplossen
Leg de leerlingen uit dat er twee punten zijn waar ze moeten stoppen voordat ze op hun bestemming aankomen.
- Geef de leerlingen een tweecijferig aftrekprobleem: 73-31=?.
- Zoek de locatie van het getal 31 op de getallenlijn. Dit is het uitgangspunt.
- Zoek de locatie van het getal 73 op de getallenlijn. Dit is het einddoel.
- "Stop" bij de eerste tiende na 31. Uw eerste stop is dus 40. Meet daarna de afstand tussen 31 en 40 en noteer het antwoord: 9.
- "Stop" bij de tienden die dichter bij 73 liggen. Uw tweede stop is dus 70. Meet vervolgens de afstand tussen 40 (eerste stop) en 70 (tweede stop) en noteer het antwoord: 30.
- "Verplaats" van 70 (tweede stop) naar je eindbestemming (73). Meet de afstand tussen beide en noteer het antwoord: 3.
- Tel deze drie resultaten bij elkaar op: 9+30+3=42. Dus 73-31=42.

Stap 3. Laat de leerlingen het driecijferige aftrekkingsprobleem oplossen
Leg bij het oplossen van aftrekproblemen met dubbele cijfers uit dat niet alleen de tussenstops toenemen, maar ook de afstand tussen elke tussenstop.
- Geef de leerlingen een driecijferig aftrekprobleem: 815-398=?.
- Zoek de locatie van het getal 398 op de getallenlijn. Dit is het startpunt.
- Zoek de locatie van het getal 815 op de getallenlijn. Dit is het einddoel.
- "Stop" bij de eerste tiende na 398. Uw eerste stop is dus 400. Meet de afstand tussen 398 en 400 en noteer het antwoord: 2.
- "Stop" bij de tienden die dichter bij 815 liggen. Dus je tweede stop is 800. Meet de afstand tussen 400 en 800 en noteer het antwoord: 400.
- "Stop" bij de tienden die dichter bij 815 liggen. Uw derde stop is dus 810. Meet de afstand tussen 800 en 810 en noteer het antwoord: 10.
- "Verplaats" vanaf de derde halte naar je eindbestemming, dit is het nummer 815. Meet de afstand en noteer het antwoord: 5.
- Tel alle getallen op die je krijgt: 2+400+10+5=417. Dus 815-398-417.






