Het wederkerige of wederkerige is erg handig in allerlei algebraïsche vergelijkingen. Als u bijvoorbeeld de ene breuk door de andere deelt, vermenigvuldigt u de eerste breuk met het omgekeerde van de tweede. U moet ook de inverse gebruiken bij het zoeken naar de vergelijking van een lijn.
Stap
Methode 1 van 3: De inverse van een breuk of geheel getal vinden
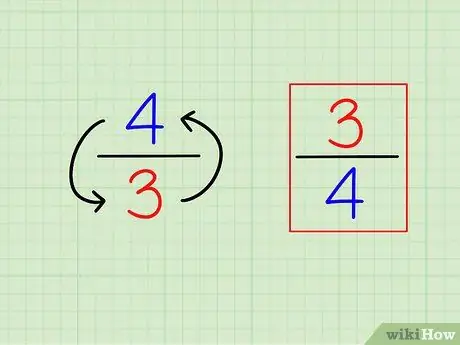
Stap 1. Vind het omgekeerde van de breuk door deze om te keren
De definitie van "wederzijds" of het tegenovergestelde is heel eenvoudig. Om het omgekeerde van een willekeurig geheel getal te vinden, berekent u eenvoudig "1 (dat getal)". Voor breuken is het omgekeerde een andere breuk, dat wil zeggen, de getallen zijn "omgekeerd" (inverse).
- Bijvoorbeeld het tegenovergestelde van 3/4 is 4/3.
- Een willekeurig getal vermenigvuldigd met zijn wederzijdse rendementen 1.
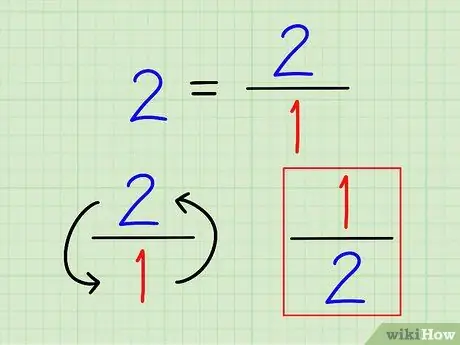
Stap 2. Schrijf het omgekeerde van het gehele getal als een breuk
Nogmaals, het omgekeerde van een getal is altijd 1 (dat getal). Voor gehele getallen, schrijf ze als breuken. Het heeft geen zin om dat getal tot een decimaal te berekenen.
Bijvoorbeeld, het omgekeerde van 2 is 1 2 = 1/2.
Methode 2 van 3: De inverse van een gemengde breuk vinden
Stap 1. Identificeer gemengde nummers
Gemengde breuken bestaan uit gehele getallen en breuken, zoals 24/5. Er zijn twee stappen om het omgekeerde van een gemengd getal te vinden, zoals hieronder beschreven.
Stap 2. Zet gemengde getallen om in onechte breuken
Onthoud dat 1 altijd kan worden geschreven als (getal)/(zelfde getal), en breuken met dezelfde noemer (onderste getal) kunnen bij elkaar worden opgeteld. Hier is een voorbeeld met 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
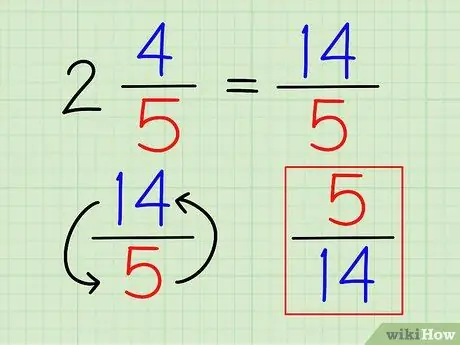
Stap 3. Draai de breuk om
Als het getal eenmaal volledig als een breuk is geschreven, kun je het omgekeerde vinden, net als elke andere breuk, door de breuk om te keren.
In het bovenstaande voorbeeld is het omgekeerde van 14/5 is 5/14.
Methode 3 van 3: Het tegenovergestelde van een decimaal vinden
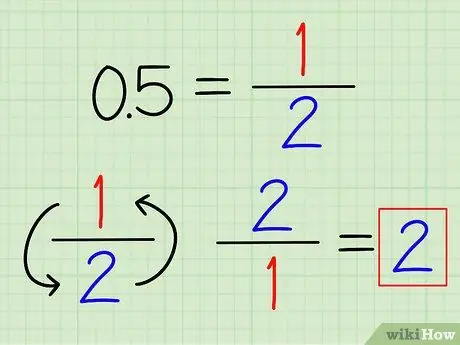
Stap 1. Converteer decimalen indien mogelijk naar breuken
U herkent misschien enkele veelgebruikte decimale getallen, die gemakkelijk kunnen worden omgezet in breuken. Bijvoorbeeld 0,5 = 1/2 en 0,25 = 1/4. Zodra het decimaalteken is omgezet in een breuk, draait u de breuk eenvoudig om om het omgekeerde te vinden.
Bijvoorbeeld, het omgekeerde van 0,5 is 2/1 = 2.
Stap 2. Schrijf een deelprobleem
Als je het niet naar een breuk kunt converteren, bereken dan het omgekeerde van het getal in de vorm van een deelprobleem: 1 (decimaal). U kunt een rekenmachine gebruiken om het op te lossen of doorgaan naar de volgende stap om het handmatig op te lossen.
U kunt bijvoorbeeld het omgekeerde van 0,4 vinden door 1 0,4 te berekenen
Stap 3. Verander het deelprobleem om hele getallen te gebruiken
De eerste stap bij het delen van decimalen is om de komma te verplaatsen totdat alle getallen hele getallen zijn. Zolang je de komma van beide getallen met hetzelfde aantal stappen verplaatst, krijg je het juiste antwoord.
U kunt bijvoorbeeld 1 0, 4 gebruiken en het herschrijven als 10 4. In dit geval verplaatst u alle decimalen één stap naar rechts, op dezelfde manier waarop u elk getal met tien vermenigvuldigt
Stap 4. Los het probleem op met staartdeling
Gebruik de staartdelingsmethode om het omgekeerde te berekenen. Als je 10 4 telt, krijg je het antwoord 2, 5 wat het omgekeerde is van 0, 4.
Tips
- De negatieve reciproke van een getal is hetzelfde als de reguliere reciproke, in die zin dat het wordt vermenigvuldigd met een negatieve. Bijvoorbeeld, de negatieve reciproke van 3/4 is -4/3.
- Het wederkerige of wederkerige wordt vaak de "inverse vermenigvuldiging" genoemd.
- Het getal 1 is het tegenovergestelde van zichzelf omdat 1 1 = 1.
- Het getal 0 heeft geen wederkerigheid omdat 0 ongedefinieerd is.
