- Auteur Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:29.
- Laatst gewijzigd 2025-01-23 12:42.
Voor de meeste mensen zijn breuken de eerste ingewikkelde berekeningen die ze tegenkomen. Het concept van breuken is vrij moeilijk en vereist dat je speciale voorwaarden leert om het te doen. Omdat breuken speciale regels hebben voor optellen, aftrekken, vermenigvuldigen en delen, zijn veel mensen hierover in de war. Met veel oefening kan iedereen echter berekeningen met betrekking tot breuken leren en voltooien.
Stap
Methode 1 van 5: Breuken begrijpen
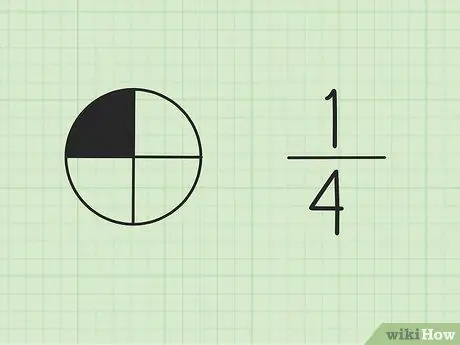
Stap 1. Begrijp dat breuken deel uitmaken van een geheel
Het getal bovenaan wordt de teller genoemd en vertegenwoordigt het aantal delen van het totaal. Het getal onderaan wordt de noemer genoemd en staat voor het totale aantal onderdelen.
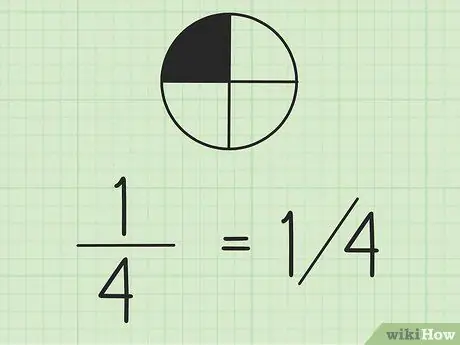
Stap 2. Houd er rekening mee dat je breuken kunt schrijven met slashes
Het getal links is de teller en het getal rechts is de noemer. Als u met breuken op dezelfde lijn werkt, is het een goed idee om de teller boven de noemer te schrijven.
Als je bijvoorbeeld een van de vier pizzapunten neemt, heb je pizza. Als je 7/3 pizza's hebt, betekent dit dat je twee hele pizza's hebt plus 1 van de 3 pizzapunten
Methode 2 van 5: Verschil tussen gemengde en eenvoudige breuken

Stap 1. Begrijp dat gemengde getallen bestaan uit gehele getallen en breuken, bijvoorbeeld 2 1/3 of 45 1/2
Gewoonlijk moet u gemengde getallen converteren naar een eenvoudigere vorm om op te tellen, af te trekken, te vermenigvuldigen of te delen.

Stap 2. Wijzig het gemengde getal door het hele getal te vermenigvuldigen met de noemer in de breuk en het vervolgens op te tellen bij de teller
Schrijf het resultaat als de teller, terwijl de noemer niet verandert.
Als u bijvoorbeeld 2 1/3 naar een eenvoudige breuk wilt converteren, vermenigvuldigt u 2 met 3, telt u 1 op en krijgt u 7/3

Stap 3. Converteer eenvoudige breuken naar gemengde getallen door de teller te delen door de noemer
Het hele resultaat van de deling wordt geschreven als een geheel getal en de rest van de deling wordt geschreven als de teller van de breuk. De noemer verandert niet.
Als u bijvoorbeeld 7/3 naar een gemengd getal wilt converteren, deelt u 7 door 3 om 2 te krijgen met een rest van 1. Het gemengde getal is dus 2 1/3. Eenvoudige breuken kunnen alleen worden omgezet in gemengde getallen als de teller groter is dan de noemer
Methode 3 van 5: Breuken optellen en aftrekken
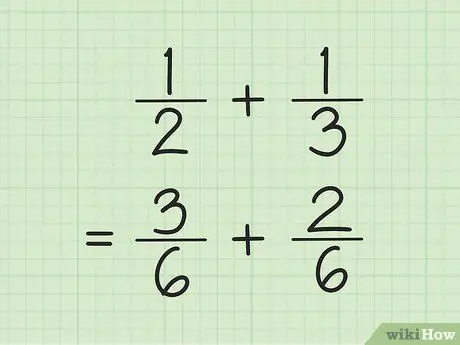
Stap 1. Zoek een gemeenschappelijke noemer om breuken op te tellen en af te trekken
De truc, vermenigvuldig de getallen in de noemer en vermenigvuldig vervolgens elke teller met het getal dat wordt gebruikt om de noemer te vinden. Soms kun je de LCM (kleinste gemene veelvoud) voor de noemer vinden door de noemers met elkaar te vermenigvuldigen.
Als u bijvoorbeeld en 1/3 wilt optellen, zoekt u eerst de LCM (kleinste gemene veelvoud) van de twee noemers door elkaar te vermenigvuldigen. U vermenigvuldigt dus 2 en 3 om LCM 6 te krijgen. Vermenigvuldig 1 met 3 om 3 te krijgen als de nieuwe teller van de eerste breuk. Vermenigvuldig 1 bij 2 om 2 te krijgen als de nieuwe teller van de tweede breuk. Je nieuwe breuken zijn 3/6 en 2/6
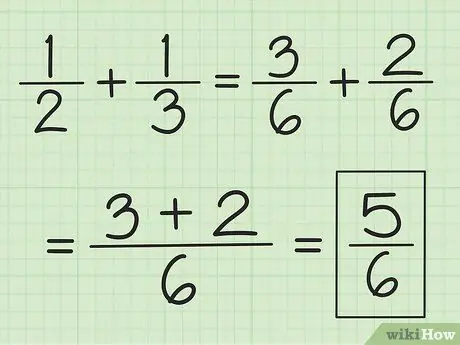
Stap 2. Tel de twee tellers bij elkaar op en verander de noemer niet
3/6 plus 2/6 is bijvoorbeeld 5/6 en 2/6 plus 1/6 is 3/6
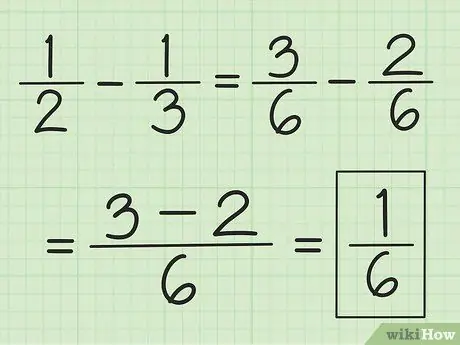
Stap 3. Gebruik een vergelijkbare techniek voor aftrekken
Zoek eerst de LCM van de noemers, maar in plaats van ze op te tellen, trek je het nummer van de eerste teller af met het nummer van de tweede.
Als u bijvoorbeeld 1/3 van 1/2 wilt aftrekken, wijzigt u eerst de breuken in 3/6 en 2/6 en trekt u vervolgens 3 bij 2 af om 1 te krijgen. Dit resulteert in 1/6
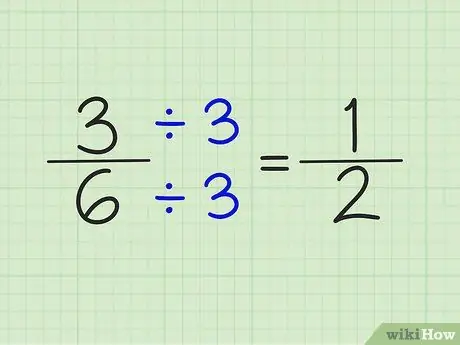
Stap 4. Vereenvoudig breuken door de teller en noemer te delen door hetzelfde getal
Het getal 5/6 kan bijvoorbeeld niet worden vereenvoudigd. 3/6 kan echter worden vereenvoudigd door de teller en noemer te delen door het getal 3. Het resultaat is een breuk van 1/2

Stap 5. Converteer de breuk naar een gemengd getal als de teller groter is dan de noemer
Methode 4 van 5: Vermenigvuldigen en delen van breuken
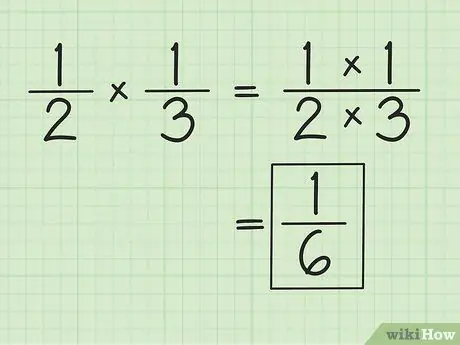
Stap 1. Vermenigvuldig de teller en de noemer afzonderlijk om breuken te vermenigvuldigen
Als u bijvoorbeeld vermenigvuldigt met 1/3, is het resultaat 1/6 (1 keer 1 en 2 keer 3). U hoeft de noemers niet te matchen bij het vermenigvuldigen van breuken. Vereenvoudig of wijzig de verkregen resultaten, indien nodig
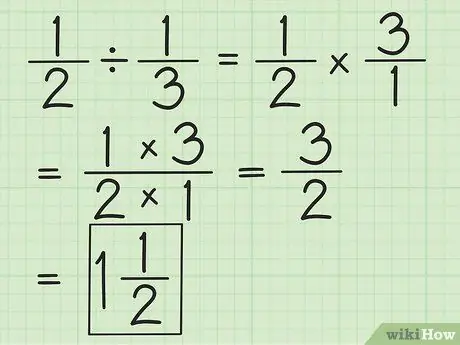
Stap 2. Deel twee breuken door de tweede breuk om te keren en vervolgens beide te vermenigvuldigen
Als u bijvoorbeeld 1/2 door 1/3 wilt delen, keert u eerst de tweede breuk om naar 3/1. Vermenigvuldig met 3/1 en krijg 3/2. Vereenvoudig breuken of converteer indien mogelijk naar gemengde getallen
Methode 5 van 5: Werken met complexe breuken
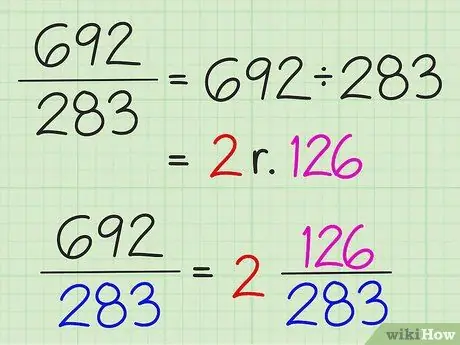
Stap 1. Bewerk alle breuken op dezelfde manier, zelfs als het probleem erg ingewikkeld lijkt
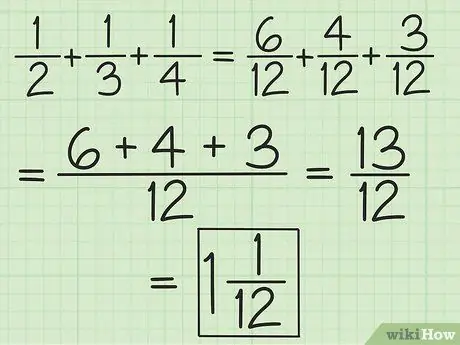
Stap 2. Zoek de noemers voor alle breuken of werk in paren van links naar rechts om meer dan twee breuken op te tellen en af te trekken
Als u bijvoorbeeld 1/2, 1/3 en 1/4 wilt optellen, kunt u ze wijzigen in 6/12, 4/12 en 3/12 om 13/12 te krijgen, of u kunt 3/6 en 2 optellen /6 zodat je 5/6 krijgt, voeg dan 5/6 en 1/4 toe (vergelijk de noemers zodat de tweede breuk 3/12 wordt) om 13/12 (10/12 plus 3/12) te krijgen. Converteer het naar een gemengd getal, dat is 1 1/12
Tips
- Vergeet niet dat je behoorlijk wat wiskunde hebt geleerd. Wiskunde is als een taal die je vloeiend kunt uitspreken, en nu probeer je die te leren lezen en schrijven.
- Vergeet niet om het eindresultaat van uw berekening altijd te vereenvoudigen, of uw probleem nu de vorm heeft van een gewone breuk, een gemengd getal of een complexe breuk.






