- Auteur Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Laatst gewijzigd 2025-06-01 06:07.
Wiskunde is moeilijk. Het is gemakkelijk om zelfs de basisconcepten te vergeten als je de vele verschillende principes en methoden probeert te onthouden. Hier zijn twee nieuwe manieren om breuken te vereenvoudigen.
Stap
Methode 1 van 4: De grootste gemeenschappelijke factor gebruiken

Stap 1. Noteer de teller- en noemerfactoren
Factoren zijn getallen die je kunt vermenigvuldigen om een ander getal te krijgen. 3 en 4 zijn bijvoorbeeld factoren van 12 omdat je ze met elkaar kunt vermenigvuldigen om 12 te krijgen. Om de factoren van een getal op te schrijven, hoef je alleen maar alle getallen op te schrijven die kunnen worden vermenigvuldigd om dat getal te krijgen, en die deelbaar zijn door de factoren.
-
Noteer de factoren van het getal van klein naar groot, zonder factor 1 te vergeten. Zo noteer je bijvoorbeeld de teller en noemer van de breuk 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Stap 2. Zoek de grootste gemene deler (GCF) van de teller en de noemer
GCF is het grootste getal dat twee of meer getallen gelijk kan verdelen. Nadat je alle factoren van het getal hebt opgeschreven, hoef je alleen nog maar het grootste getal te vinden dat hetzelfde is in beide lijsten met factoren.
-
24: 1, 2, 3, 4, 6,
Stap 8., 12, 24.
-
32: 1, 2, 4,
Stap 8., 16, 32.
-
De GCF van 24 en 32 is 8 omdat 8 het grootste getal is dat 24 en 32 gelijkmatig kan verdelen.

Stap 3. Deel de teller en breuk door de GCF
Nu je de GCF hebt, hoef je alleen maar de teller en de noemer door dat getal te delen om je breuk te vereenvoudigen tot de eenvoudigste vorm. Hier is hoe het te doen:
- 24/8 = 3
- 32/8 = 4
- De eenvoudige breuk is 3/4.

Stap 4. Controleer je werk
Als je er zeker van wilt zijn dat je de breuk correct hebt vereenvoudigd, hoef je alleen maar de nieuwe teller en noemer te vermenigvuldigen met hun GCF om de oorspronkelijke breuk terug te krijgen. Hier is hoe het te doen:
- 3 * 8 = 24
- 4 * 8 = 32
-
U bent teruggekeerd naar de oorspronkelijke vorm, namelijk 24/32.
U kunt ook de breuk controleren om er zeker van te zijn dat deze niet verder vereenvoudigd kan worden. Aangezien 3 een priemgetal is, kan het alleen worden gedeeld door 1 en zichzelf, en is vier niet deelbaar door 3, dus de breuk kan niet verder worden vereenvoudigd
Methode 2 van 4: Blijf delen door kleine getallen

Stap 1. Kies een klein aantal
Bij deze methode hoeft u slechts een klein aantal te kiezen, zoals 2, 3, 4, 5 of 7, om mee te beginnen. Kijk naar de breuken om er zeker van te zijn dat elk deel deelbaar is door het getal dat je hebt gekozen. Als je bijvoorbeeld een breuk 24/108 hebt, kies dan geen 5 omdat ze niet deelbaar zijn door 5. Als je echter een breuk 25/60 hebt, is 5 het juiste getal om te gebruiken.
Voor de breuk 24/32 is 2 een goed getal. Omdat beide getallen even getallen zijn, zijn ze deelbaar door 2

Stap 2. Deel de teller en noemer van de breuk door het getal
De nieuwe breuk zal bestaan uit een nieuwe teller en noemer, die je krijgt nadat je de boven- en onderkant van de breuk 24/32 door 2 hebt gedeeld. Zo doe je dat:
- 24/2 = 12
- 32/2 = 16
- Je nieuwe breuk is 12/16.
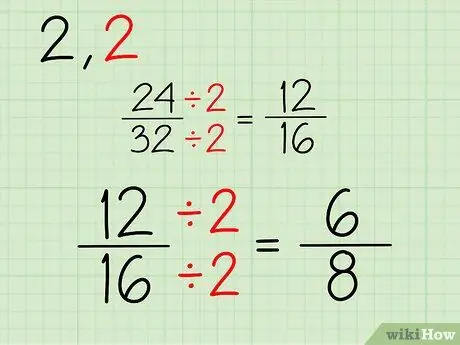
Stap 3. Herhaal
Ga door met dit proces. Aangezien beide getallen even getallen zijn, kun je blijven delen door 2. Als een of beide tellers en noemers oneven getallen zijn, kun je proberen te delen door een ander getal. Hier is het proces voor het vereenvoudigen van de 12/16-breuk:
- 12/2 = 6
- 16/2 = 8
- Je nieuwe breuk is 6/8.

Stap 4. Blijf het getal delen totdat het niet meer deelbaar is
De nieuwe teller en noemer zijn ook even getallen, dus je kunt blijven delen door 2. Zo doe je het:
- 6/2 = 3
- 8/2 = 4
- Je nieuwe breuk is 3/4.

Stap 5. Zorg ervoor dat de breuk niet verder vereenvoudigd kan worden
In de breuk 3/4 is 3 een priemgetal, dus de factoren zijn alleen 1 en zichzelf, en 4 is niet deelbaar door 3, dus de breuk kan niet verder worden vereenvoudigd. Als de teller of noemer van de breuk niet meer kan worden gedeeld door het getal dat je hebt geselecteerd, kun je deze mogelijk nog steeds delen door een ander getal.
Als je bijvoorbeeld de breuk 10/40 hebt en je deelt de teller en noemer door 5, dan is het resultaat 2/8. Je kunt de teller en breuk niet blijven delen door 5, maar je kunt beide delen door 2, zodat het eindresultaat 1/4 is

Stap 6. Controleer je werk
Vermenigvuldig 3/4 met 2/2 opnieuw drie keer, om er zeker van te zijn dat u de eerste breuk krijgt, namelijk 24/32. Hier is hoe het te doen:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Merk op dat je 24/32 deelt door 2 * 2 * 2, wat hetzelfde is als delen door 8, de grootste GCF van 24 en 32.
Methode 3 van 4: De factoren schrijven

Stap 1. Schrijf je breuk op
Laat een grote ruimte aan de rechterkant van je papier - je hebt het nodig om de factoren op te schrijven.

Stap 2. Noteer de factoren van de teller en noemer
Alleen de factoren van de twee. De eenvoudigste manier is om de factoren op elkaar te schrijven. Begin met het cijfer 1 en schrijf de factoren op.
-
Als uw breuk bijvoorbeeld 24/60 is, begin dan met 24.
Schrijf op: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
Dan het getal 60.
Schrijf op: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Stap 3. Zoek en deel door de grootste gemene deler
Deze term kan in uw gedrukte boek worden geschreven als GCF. Wat is het grootste getal dat de teller en de noemer kan delen? Wat het getal ook is, deel beide getallen door dat getal.
Voor ons voorbeeld is het grootste getal dat een factor is van beide getallen 12. Dus delen we 24 bij 12 en 60 bij 12, wat ons 2/5 geeft - onze eenvoudige breuk
Methode 4 van 4: Een priemfactorboom gebruiken

Stap 1. Zoek de priemfactoren van de teller en noemer
Een priemgetal is een getal dat niet kan worden gedeeld door een ander getal (behalve zichzelf en 1, natuurlijk). 2, 3, 5, 7 en 11 zijn voorbeelden van priemgetallen.
- Begin met de teller. Vanaf 24, gesplitst in 2 en 12. Aangezien 2 al een priemgetal is, hoef je het niet meer te delen! Breek 12 dan in 2 getallen: 2 en 6. 2 zijn priemgetallen - geweldig! Verdeel nu 6 in 2 getallen: 2 en 3. Je hebt nu 2, 2, 2 en 3 als priemgetallen.
- Werk nu aan de noemer. Splits vanaf 60 je boom in 2 en 30. 30 verdeel dan in 2 en 15. Verdeel vervolgens 15 in 3 en 5, beide priemgetallen. Nu heb je 2, 2, 3 en 5 als priemgetallen.
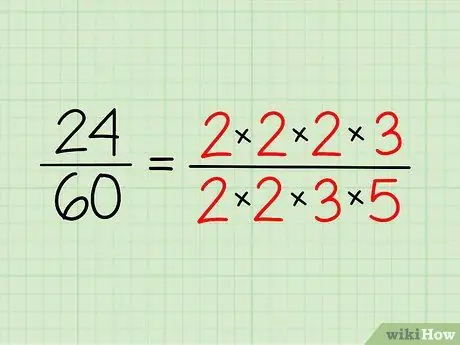
Stap 2. Noteer de priemfactorisatie van elk getal
Noteer de priemgetallen die je hebt voor elk nummer en schrijf ze in vermenigvuldigingsvorm. Je hoeft het niet te vermenigvuldigen - het is gewoon een manier om het gemakkelijker te zien.
- Dus voor 24 heb je 2 x 2 x 2 x 3 = 24.
- Voor 60 heb je 2 x 2 x 3 x 5 = 60

Stap 3. Elimineer dezelfde factoren
Elk nummer dat deel uitmaakt van beide nummers kan worden weggegooid. In dit voorbeeld zijn de gelijke factoren een paar 2en en één 3. Tot ziens!
- De rest is 2 en 5 - of 2/5! Hetzelfde antwoord kregen we de weg hierboven.
- Als de teller en noemer van de breuk even getallen zijn, deel dan niet gewoon door twee. Ga door met het delen totdat het getal dat je krijgt niet meer gedeeld kan worden.






