- Auteur Jason Gerald [email protected].
- Public 2023-12-16 11:29.
- Laatst gewijzigd 2025-01-23 12:42.
De vierkantswortel van een getal is gemakkelijk te vinden als het antwoord een geheel getal is. Als het antwoord geen geheel getal is, is er een reeks processen die u kunt volgen om de vierkantswortel te krijgen, zelfs als u geen rekenmachine gebruikt. Daarvoor moet je de basisprincipes van vermenigvuldigen, optellen en delen begrijpen.
Stap
Methode 1 van 3: De vierkantswortel van een geheel getal vinden
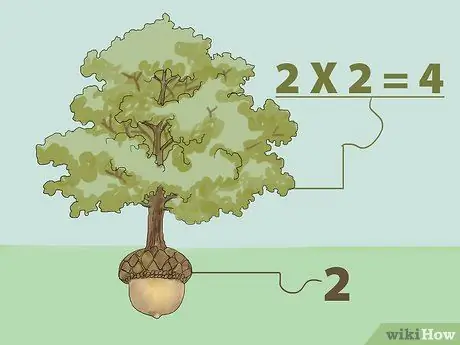
Stap 1. Vind de perfecte vierkantswortel door te vermenigvuldigen
De vierkantswortel van een getal is een getal dat, wanneer het met zichzelf wordt vermenigvuldigd, het oorspronkelijke getal oplevert. Met andere woorden: "Welk getal kunnen we met zichzelf vermenigvuldigen om het gewenste getal te krijgen?"
- De vierkantswortel van 1 is bijvoorbeeld 1 omdat 1 vermenigvuldigd met 1 1 is (1X1=1). Dus de vierkantswortel van 4 is 2 omdat 2 vermenigvuldigd met 2 4 is (2X2=4). Zie het vierkantswortelconcept als een boom. Een boom groeit uit zaad. Dus een boom is groter dan een zaadje, dat groeit uit een zaadje dat zijn wortel is. Uit het bovenstaande voorbeeld is 4 de boom en 2 het zaad.
- Dus de vierkantswortel van 9 is 3 (3X3=9), van 16 is 4 (4X4=16), van 25 is 5 (5X5=25), van 36 is 6 (6X6=36), van 49 is 7 (7X7 =49), van 64 is 8 (8X8=64), van 81 is 9 (9X9=81), en van 100 is 10 (10X10=100).
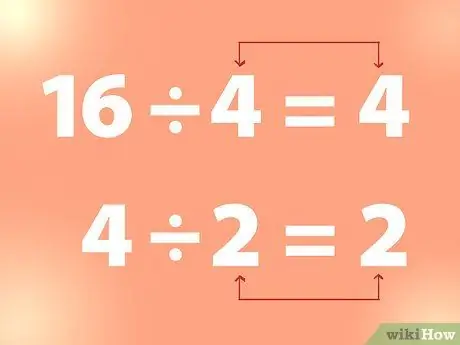
Stap 2. Gebruik continue deling om de vierkantswortel te vinden
Om de vierkantswortel van een geheel getal te vinden, kun je het gehele getal delen door een getal totdat je een getal krijgt dat gelijk is aan de deler.
- Voorbeeld: 16 gedeeld door 4 is 4. En 4 gedeeld door 2 is 2, enzovoort. Dus uit het bovenstaande voorbeeld is 4 de vierkantswortel van 16 en 2 is de vierkantswortel van 4.
- Perfecte vierkantswortels hebben geen breuken of decimalen omdat het hele getallen zijn.
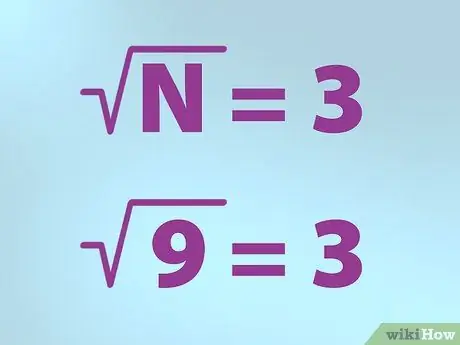
Stap 3. Gebruik het juiste symbool voor de vierkantswortel
Wiskundigen gebruiken een speciaal symbool om de vierkantswortel weer te geven. De vorm is als een vinkje met plus een lijn rechtsboven.
- N is gelijk aan het getal waarvan u de vierkantswortel wilt vinden. N wordt onder het vinkje geplaatst.
- Dus, als je de vierkantswortel van 9 wilt vinden, schrijf dan een formule door "N" (9) binnen een vinkje (symbool "root") te plaatsen, schrijf dan een gelijkteken en gevolgd door 3. Het betekent "vierkantswortel van 9 is gelijk aan 3".
Methode 2 van 3: De vierkantswortel van een ander getal vinden
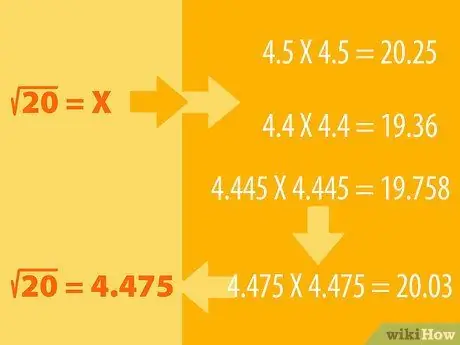
Stap 1. Raad en voer het eliminatieproces uit
Het is moeilijk om de vierkantswortel van een niet-geheel getal te vinden. Dat betekent echter niet dat het onmogelijk is.
- Stel dat u bijvoorbeeld de vierkantswortel van 20 wilt vinden. We weten dat 16 een perfect vierkant is waarvan de vierkantswortel 4 is (4X4=16). Dan zijn de 25 vierkantswortels 5 (5X5=25), dus de vierkantswortel van 20 moet tussen de twee liggen.
- Je kunt raden dat de vierkantswortel van 20 4,5 is, nu vierkant 4,5 om het resultaat te zien. Dat wil zeggen, we vermenigvuldigen 4, 5 met zichzelf: 4, 5X4, 5. Kijk of het antwoord meer of minder is dan 20. Als je gok te ver is, probeer dan een ander getal (bijv. 4, 6 of 4, 4) en pas aan de gok dienovereenkomstig. u totdat u het getal 20 krijgt.
- Bijvoorbeeld 4, 5X4, 5 = 20, 25, dus logischerwijs moeten we een kleiner getal vinden, misschien 4, 4. 4, 4X4, 4 = 19, 36. Dus de vierkantswortel van 20 moet tussen 4 liggen, 5 en 4, 4. Probeer met 4, 445X4, 445. Het resultaat is 19, 758. Het resultaat komt steeds dichterbij. Blijf proberen met andere getallen totdat je 4, 475X4, 475 = 20, 03 krijgt. Afgerond naar boven is dat getal gelijk aan 20.

Stap 2. Gebruik het middelingsproces
Dit proces begint ook met het vinden van de twee dichtstbijzijnde perfecte vierkanten die worden geflankeerd door het nummer.
- Deel dat getal vervolgens door een van de perfecte vierkantswortels. Neem het antwoord en zoek het gemiddelde tussen dat getal en het getal waarvan je de wortel wilt vinden (je kunt het gemiddelde vinden door de twee bij elkaar op te tellen en door twee te delen). Deel vervolgens het eerste getal door het verkregen gemiddelde. De laatste stap, zoek het gemiddelde van de resultaten met het gemiddelde dat de eerste keer is berekend.
- Klinkt ingewikkeld? Het zou makkelijker zijn als je een voorbeeld zou geven. 10 ligt bijvoorbeeld tussen de twee perfecte vierkanten 9 (3X3=9) en 16 (4X4=16). De vierkantswortels van beide getallen zijn 3 en 4. Dus deel 10 door het eerste getal, 3. Het resultaat is 3, 33. Zoek nu het gemiddelde van 3 en 3, 33 door ze bij elkaar op te tellen en te delen door 2. Het resultaat is 3, 1667 Deel nu 10 door 3.1667. Het resultaat is 3.1579. Zoek dan het gemiddelde van 3.1579 en 3.1667 door ze op te tellen en te delen door 2. Het resultaat is 3.1623.
- Controleer je resultaat door het antwoord (in dit voorbeeld 3, 1623) met zichzelf te vermenigvuldigen. Het resultaat van 3.1623 vermenigvuldigd met 3.1623 blijkt 10.001 te zijn.
Methode 3 van 3: Negatieve getallen kwadrateren
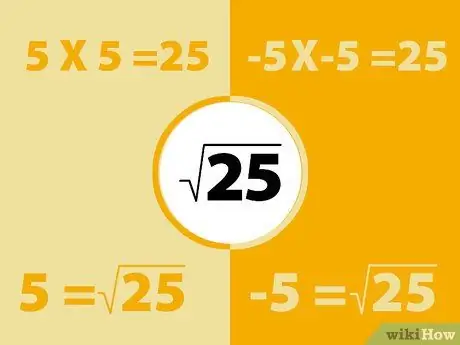
Stap 1. Vierkant negatieve getallen met dezelfde methode
Onthoud dat negatief keer negatief positief is. Dus het kwadraat van een negatief getal levert een positief getal op.
- Bijvoorbeeld -5X-5 = 25. Onthoud echter ook dat 5x5=25. Dus de vierkantswortel van 25 kan -5 of 5 zijn. In principe heeft elk getal twee vierkantswortels.
- Evenzo, 3X3=9 en -3X-3=9, dus de vierkantswortels van 9 zijn 3 en -3. De positieve vierkantswortel wordt de "hoofdwortel" genoemd. Op dit punt moeten we alleen aandacht besteden aan dit antwoord.
Stap 2. Gebruik een rekenmachine
Hoewel het het beste is om de wiskunde met de hand te doen, zijn er veel online rekenmachines beschikbaar voor het berekenen van vierkantswortels.
- Zoek naar de vierkantswortelknop op een gewone rekenmachine.
- Voer in de online calculator direct het getal in waarvan je de vierkantswortel wilt vinden en klik op de knop. De computer toont u de vierkantswortelwaarde.
Tips
-
Houd altijd een paar belangrijke perfecte vierkanten in gedachten:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Onthoud ook dit perfecte vierkant: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Let ook op dit: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






